题目内容
15.在△ABC中,已知点D在BC上,且CD=2BD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=( )| A. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$ | B. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | D. | -$\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |
分析 可画出图形,根据条件有$\overrightarrow{CD}=2\overrightarrow{DB}$,将$\overrightarrow{CD}=\overrightarrow{AD}-\overrightarrow{AC}$,$\overrightarrow{DB}=\overrightarrow{AB}-\overrightarrow{AD}$带入,并解出$\overrightarrow{AD}$,这样即可用$\overrightarrow{a},\overrightarrow{b}$表示出$\overrightarrow{AD}$,从而找出正确选项.
解答 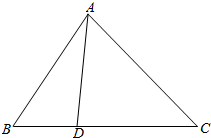 解:如图,CD=2BD;
解:如图,CD=2BD;
∴$\overrightarrow{CD}=2\overrightarrow{DB}$;
∴$\overrightarrow{AD}-\overrightarrow{AC}=2(\overrightarrow{AB}-\overrightarrow{AD})$;
∴$\overrightarrow{AD}=\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}=\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$.
故选C.
点评 考查向量数乘的几何意义,向量减法的几何意义,以及向量的数乘运算.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
3.已知定义在(0,+∞)上的函数满足xf′(x)+(2-x)f(x)=$\frac{{e}^{x}}{x}$(x+lnx-1),则下列不等式一定正确的是( )
| A. | 4f(1)<$\sqrt{e}$f($\frac{1}{2}$) | B. | 4f(2)<ef(1) | C. | 4ef(2)>9f(3) | D. | e${\;}^{\frac{3}{2}}$f($\frac{1}{2}$)<16f(2) |
10.若集合A={x|x2-1<0},B={x丨0<x<4},则A∪B等于( )
| A. | {x|0<x<l} | B. | {x|-l<x<l} | C. | {x|-1<x<4} | D. | {x|l<x<4} |