Question

3．自驾游从A地到B地有甲乙两条线路，甲线路是A-C-D-B，乙线路是A-E-F-G-H-B，其中CD段，EF段，GH段都是易堵车路段．假设这三条路段堵车与否相互独立．这三条路段的堵车概率及平均堵车时间如表所示：

堵车时间（小时）	频数
[0，1]	8
（1，2]	6
（2，3]	38
（3，4]	24
（4，5]	24

经调查发现堵车概率x在（$\frac{2}{3}$，1）上变化，y在（0，$\frac{1}{2}$）上变化．在不堵车的状况下，走甲路线需汽油费500元，走乙线路需汽油费545元．而每堵车1小时，需多花汽油费20元．路政局为了估计CD段平均堵车时间，调查了100名走甲线路的司机，得到如表数据．

路段	CD	EF	GH
堵车概率	x	y	$\frac{1}{4}$
平均堵车时间（小时）	a	2	1

（Ⅰ）求CD段平均堵车时间a的值，（同一组数据用该区间的中点值做代表）
（Ⅱ）若走甲、乙路线所花汽油费的期望值相等，且x=$\frac{11}{12}$，求y的值．

Answer 1

分析 （1）由已知数据能画出CD段堵车时间频率分布直方图，用总的堵车时间除以总人数100人，即得到平均堵车时间；
（2）利用走甲、乙路线所花汽油费的期望值相等，可得550+4y=500（1-x）+（500+60）x，即6x-4y-5=0，即可得出结论．

解答 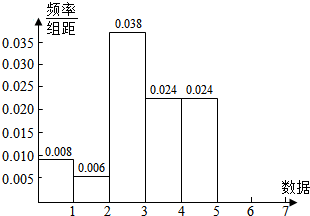解：（1）由CD段平均堵车时间，调查了100名走甲线路的司机，得到数据统计表，
作出CD段堵车时间频率分布直方图，如右图．
a=0.5×$\frac{8}{100}$+1.5×$\frac{6}{100}$+2.5×$\frac{38}{100}$+3.5×$\frac{24}{100}$+4.5$\frac{24}{100}$=3．
（2）在EF路段多花汽油费的数学期望是20×2y=40y元，在GH路段多花汽油费的数学期望是20×1×$\frac{1}{4}$=5元，
∵EF，GH路段堵车与否相互独立，
∴走乙路线多花汽油费的数学期望是40y+5元，
∴走乙路线花汽油费的数学期望是40y+550元，
∵走甲、乙路线所花汽油费的期望值相等，
∴550+4y=500（1-x）+（500+60）x，即6x-4y-5=0，
∵x=$\frac{11}{12}$，
∴y=$\frac{1}{8}$

点评 本题考查概率的计算，考查面积的计算，考查学生分析解决问题的能力，属于中档题．