题目内容
9.已知a,b∈R,f(x)=|x-2|-|x-1|.(1)若f(x)>0,求实数x的取值范围;
(2)对?b∈R,若|a+b|+|a-b|≥f(x)恒成立,求a的取值范围.
分析 (1)利用绝对值不等式的解法,化简为二次不等式求解即可.
(2)求出不等式的左侧的最小值与右侧的最大值,转化为绝对值不等式求解即可.
解答 解:(1)由f(x)>0得|x-2|>|x-1|,
两边平方得x2-4x+4>x2-2x+1,
解得$x<\frac{3}{2}$,即实数x的取值范围是$(-∞,\frac{3}{2})$…(5分)
(2)|a+b|+|a-b|≥|a+b+a-b|=2|a|,
∵f(x)=|x-2|-|x-1|=$\left\{\begin{array}{l}{-1,x≥2}\\{3-2x,1≤x<2}\\{1,x<1}\end{array}\right.$,f(x)max=1,
∴$2|a|≥1⇒|a|≥\frac{1}{2}⇒a≥\frac{1}{2}或a≤-\frac{1}{2}$.
所以a的取值范围为$(-∞,-\frac{1}{2}]∪[\frac{1}{2},+∞)$…(10分)
点评 本题考查绝对值不等式的解法,函数恒成立条件的应用,分段函数的应用,考查转化思想以及计算能力.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
1.定积分$\int_0^2{[\sqrt{4-{{(x-2)}^2}}-x]dx}$的值为( )
| A. | $\frac{π-2}{4}$ | B. | π-2 | C. | 2π-2 | D. | 4π-8 |
19.已知等差数列{an}满足a3+a4=12,3a2=a5,则a5=( )
| A. | 3 | B. | 6 | C. | 9 | D. | 11 |
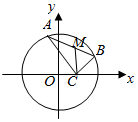 已知点C(1,0),点A,B是⊙O:x2+y2=9上任意两个不同的点,且满足$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,设M为弦AB的中点.
已知点C(1,0),点A,B是⊙O:x2+y2=9上任意两个不同的点,且满足$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,设M为弦AB的中点.