题目内容
6．已知集合A={x|-3≤1-2x＜3}，集合B={x|y=lg（x-1）}，则A∩B等于（ ）| A． | {x|-2＜x≤1} | B． | {x|1＜x＜2} | C． | {x|1＜x≤2} | D． | {x|-1≤x＜2} |
分析 求出A中不等式的解集确定出A，求出B中x的范围确定出B，找出两集合的交集即可．
解答 解：∵A={x|-3≤1-2x＜3}={x|-1＜x≤2}，B={x|y=lg（x-1）}={x|x＞1}，
∴A∩B={x|-1＜x≤2}∩{x|x＞1}={x|1＜x≤2}．
故选：C．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
16．计算：$\int_1^2{{{（x-1）}^5}dx}$=（ ）
| A． | $-\frac{1}{5}$ | B． | $\frac{1}{5}$ | C． | $-\frac{1}{6}$ | D． | $\frac{1}{6}$ |
14．偶函数f（x）（x∈R）满足：f（4）=f（1）=0，且在区间[0，3]与[3，+∞）上分别递减和递增，则不等式xf（x）＜0的解集为（ ）
| A． | （-∞，-4）∪（4，+∞） | B． | （-∞，-4）∪（-1，0） | C． | （-4，-1）∪（1，4） | D． | （-∞，-4）∪（-1，0）∪（1，4） |
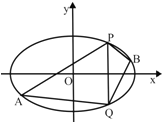如图．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的离心率e=$\frac{1}{2}$，椭圆C上一点M到左、右两个焦点F1、F2的距离之和是4．