题目内容
3.已知函数f(x)=ax+lnx.(Ⅰ)若f(x)在区间(0,1)上单调递增,求实数a的取值范围;
(Ⅱ)设函数h(x)=-$\frac{1}{2}$x2-f(x)有两个极值点x1、x2,且x1∈[$\frac{1}{2}$,1),求证:|h(x1)-h(x2)|<2-ln2.
分析 (I)令f′(x)≥0在(0,1)上恒成立,使用分离参数法求出a的范围;
(II)令h′(x)=0,结合二次函数的性质和极值点的定义可判断h(x1)<h(x2),根据根与系数的关系化简|h(x1)-h(x2)|=-$\frac{1}{2}$x12+$\frac{1}{2{{x}_{1}}^{2}}$+2lnx1,求出右侧函数的最大值即可证明结论.
解答 解:(I)∵f(x)在区间(0,1)上单调递增,
∴f′(x)=a+$\frac{1}{x}$≥0,x∈(0,1),
即a$≥-\frac{1}{x}$,
∵x∈(0,1),∴-$\frac{1}{x}$<-1,
∴a≥-1.
(II)证明:h(x)=-$\frac{1}{2}{x}^{2}$-ax-lnx,h′(x)=-x-a-$\frac{1}{x}$,x∈(0,+∞).
令h′(x)=0得x2+ax+1=0,
∵函数h(x)=-$\frac{1}{2}$x2-f(x)有两个极值点x1、x2,且x1∈[$\frac{1}{2}$,1),
∴方程x2+ax+1=0有两解x1、x2,且x1∈[$\frac{1}{2}$,1),
∴x1•x2=1,x1+x2=-a,且ax1=-1-x12,ax2=-1-x22,x2∈(1,2].
∴当0<x<x1时,h′(x)<0,当x1<x<x2时,h′(x)>0,当x>x2时,h′(x)<0,
∴x1为h(x)的极小值点,x2为h(x)的极大值点,
∴|h(x1)-h(x2)|=h(x2)-h(x1)=-$\frac{1}{2}$x22-ax2-lnx2+$\frac{1}{2}$x12+ax1+lnx1
=$\frac{1}{2}$x22-$\frac{1}{2}$x12+ln$\frac{{x}_{1}}{{x}_{2}}$=-$\frac{1}{2}$x12+$\frac{1}{2{{x}_{1}}^{2}}$+2lnx1,
令H(x1)=-$\frac{1}{2}$x12+$\frac{1}{2{{x}_{1}}^{2}}$+2lnx1,
则H′(x1)=-x1-$\frac{1}{{{x}_{1}}^{3}}$+$\frac{2}{{x}_{1}}$=$\frac{-{{x}_{1}}^{4}+2{{x}_{1}}^{2}-1}{{{x}_{1}}^{3}}$=-$\frac{({{x}_{1}}^{2}-1)^{2}}{{{x}_{1}}^{3}}$<0,
∴H(x1)在[$\frac{1}{2}$,0)上是减函数,
∴H(x1)≤H($\frac{1}{2}$)=$\frac{15}{8}$-2ln2<2-ln2,
即|h(x1)-h(x2)|<2-ln2.
点评 本题考查了导数与函数单调性的关系,函数极值的判断,函数恒成立问题研究,属于难题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | $\frac{π}{27}$ | B. | $\frac{8π}{27}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{9}$ |
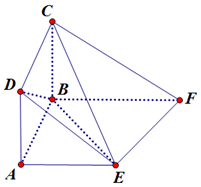 在如图所示的多面体ABCDEF中,四边形ABCD为正方形,底面ABFE为直角梯形,∠ABF为直角,$AE∥BF,AB=\frac{1}{2}BF=1$,
在如图所示的多面体ABCDEF中,四边形ABCD为正方形,底面ABFE为直角梯形,∠ABF为直角,$AE∥BF,AB=\frac{1}{2}BF=1$,



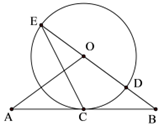 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.