题目内容
2.若x∈[1,+∞)时,关于x的不等式$\frac{xlnx}{x+1}$≤λ(x-1)恒成立,则实数λ的取值范围为[$\frac{1}{2}$,+∞).分析 把不等式转化为xlnx-λ(x2-1)≤0,设函数f(x)=xlnx-λ(x2-1),从而对任意x∈[1,+∞),不等式f(x)≤0=f(1)恒成立,求出f′(x),对λ分类判断f′(x)的符号得答案.
解答 解:x∈[1,+∞)时,$\frac{xlnx}{x+1}$≤λ(x-1)?xlnx-λ(x2-1)≤0,
设函数f(x)=xlnx-λ(x2-1),从而对任意x∈[1,+∞),不等式f(x)≤0=f(1)恒成立,
又f′(x)=lnx+1-2λx.
①当f′(x)=lnx+1-2λx≤0,即$\frac{lnx+1}{x}≤2λ$时,函数f(x)单调递减,设g(x)=$\frac{lnx+1}{x}$,则g′(x)=$\frac{-lnx}{{x}^{2}}≤0$,g(x)max=g(1)=1,
即1≤2λ,∴$λ≥\frac{1}{2}$,符合题意;
②当λ≤0时,f′(x)=lnx+1-2λx≥0恒成立,此时f(x)单调递增,于是不等式f(x)≥f(1)=0对任意x∈[1,+∞)恒成立,不符合题意;
③当0<λ<$\frac{1}{2}$时,设h(x)=f′(x)=lnx+1-2λx,则h′(x)=$\frac{1}{x}-2λ=0$,可得x=$\frac{1}{2λ}$>1.
当x∈(1,$\frac{1}{2λ}$)时,h′(x)=$\frac{1}{x}-2λ$>0,此时h(x)=f′(x)=lnx+1-2λx单调递增,∴f′(x)=lnx+1-2λx>f′(1)=1-2λ>0,
故当x∈(1,$\frac{1}{2λ}$)时,函数f(x)单调递增,于是,当x∈(1,$\frac{1}{2λ}$)时,f(x)>0恒成立,不符合题意.
综上所述,实数λ的取值范围为[$\frac{1}{2}$,+∞).
故答案为:[$\frac{1}{2}$,+∞).
点评 本题考查恒成立问题,训练了分离参数法,考查利用导数求函数在闭区间上的最值,属难题.

 阅读快车系列答案
阅读快车系列答案 如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{11}$ | D. | $\frac{4}{13}$ |
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
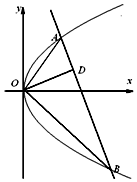 如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).
如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点). 某人上午7时乘船出发,以匀速v海里/小时(4≤v≤20)从A港前往相距50海里的B地,然后乘汽车以匀速ω千米/小时(30≤ω≤100)自B港前往相距300千米的C市,计划当天下午4到9时到达C市.设乘船和汽车的所要的时间分别为x、y小时,如果所需要的经费P=100+3(5-x)+(8-y)(单位:元)
某人上午7时乘船出发,以匀速v海里/小时(4≤v≤20)从A港前往相距50海里的B地,然后乘汽车以匀速ω千米/小时(30≤ω≤100)自B港前往相距300千米的C市,计划当天下午4到9时到达C市.设乘船和汽车的所要的时间分别为x、y小时,如果所需要的经费P=100+3(5-x)+(8-y)(单位:元) 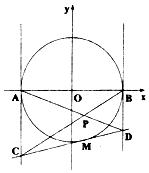 已知圆O:x2+y2=4与x轴交于A,B两点,点M为圆O上异于A,B的任意一点,圆O在点M处的切线与圆O在点A,B处的切线分别交于C,D,直线AD和BC交于点P,设P点的轨迹为曲线E.
已知圆O:x2+y2=4与x轴交于A,B两点,点M为圆O上异于A,B的任意一点,圆O在点M处的切线与圆O在点A,B处的切线分别交于C,D,直线AD和BC交于点P,设P点的轨迹为曲线E.