题目内容
20.不等式组$\left\{\begin{array}{l}{x-y-2≤0}\\{x+y+3≤0}\\{1≤|x+3|≤2}\end{array}\right.$表示的平面区域的面积为2.分析 由不等式组作出平面区域为梯形及其内部,联立方程组求出B,C,D,A的坐标,然后求解即可.
解答 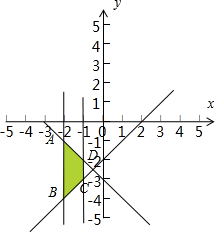 解:由不等式组$\left\{\begin{array}{l}{x-y-2≤0}\\{x+y+3≤0}\\{1≤|x+3|≤2}\end{array}\right.$作平面区域如图,
解:由不等式组$\left\{\begin{array}{l}{x-y-2≤0}\\{x+y+3≤0}\\{1≤|x+3|≤2}\end{array}\right.$作平面区域如图,
由$\left\{\begin{array}{l}{x=-2}\\{x+y+3=0}\end{array}\right.$解得A(-2,-1),由$\left\{\begin{array}{l}{x=-1}\\{x-y-2=0}\end{array}\right.$解得C(-1,-3),
由$\left\{\begin{array}{l}{x=-2}\\{x-y-2=0}\end{array}\right.$解得B(-2,-4).由$\left\{\begin{array}{l}{x=-1}\\{x+y+3=0}\end{array}\right.$D(-1,-2)
∴|AB|=3.|CD|=1,梯形的高为1,
不等式组$\left\{\begin{array}{l}{x-y-2≤0}\\{x+y+3≤0}\\{1≤|x+3|≤2}\end{array}\right.$表示的平面区域的面积为:$\frac{3+1}{2}×1$=2.
故答案为:2.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
8.在△ABC中,内角A,B,C的对边分别为a,b,c.若asinBcosC+csinBcosA=$\frac{1}{2}$b且a>b,则B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
5.“0<x<5”是“-2<x<6”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.