题目内容
15.设a>0,b>0,若1是2a与2b的等差中项,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )| A. | 8 | B. | 4 | C. | 1 | D. | $\frac{1}{4}$ |
分析 根据1是2a与2b的等差中项建立关系,2a+2b=2,即a+b=1,利用“乘1法”与基本不等式的性质即可得出.
解答 解:由题意:1是2a与2b的等差中项,则2a+2b=2,即a+b=1.
那么($\frac{1}{a}$+$\frac{1}{b}$)×1=($\frac{1}{a}$+$\frac{1}{b}$)(a+b)=2+$\frac{a}{b}+\frac{b}{a}$.
∵a>0,b>0,
∴$\frac{a}{b}+\frac{b}{a}$≥2$\sqrt{\frac{a}{b}×\frac{b}{a}}$=2,(当且仅当a=b=$\frac{1}{2}$时取等号)
故得$\frac{1}{a}$+$\frac{1}{b}$的最小值为4.
故选B.
点评 本题考查了等差中项的性质以及“乘1法”与基本不等式的性质,属于基础题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
3.若tanθ=$\frac{1}{3}$,则cos2θ=( )
| A. | $-\frac{4}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{5}$ |
20.若函数y=f(x)与y=3-x的图象关于直线y=x对称,则函数y=f(4x-x2)的增区间为( )
| A. | (2,4) | B. | (0,2) | C. | (-∞,2) | D. | (2,+∞) |
4.设a=20.3,b=0.22,c=logx(x2+0.3)(x>1),则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | b<c<a |
5.已知A={1,3,9,27,81},B={y|y=log3x,x∈A},则A∩B=( )
| A. | {1,3} | B. | {3,27,81} | C. | {1,3,9} | D. | {9,27} |
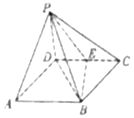 如图,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=$\frac{π}{3}$,PA=PD,点E为CD边的中点,BD⊥PE.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=$\frac{π}{3}$,PA=PD,点E为CD边的中点,BD⊥PE.