题目内容
16.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的短轴长为2$\sqrt{3}$,右焦点为F(1,0),点M是椭圆C上异于左、右顶点A,B的一点.(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线AM与直线x=2交于点N,线段BN的中点为E.证明:点B关于直线EF的对称点在直线MF上.
分析 (Ⅰ)由题意可知b=$\sqrt{3}$,c=1,a2=b2+c2=4,即可求得椭圆方程;
(Ⅱ)由“点B关于直线EF的对称点在直线MF上”等价于“EF平分∠MFB”设直线AM的方程,代入椭圆方程,由韦达定理求得M点坐标,分类讨论,当MF⊥x轴时,求得k的值,即可求得N和E点坐标,求得点E在∠BFM的角平分线所在的直线y=x-1或y=-x+1,则EF平分∠MFB,当k≠$\frac{1}{2}$时,即可求得直线MF的斜率及方程,利用点到直线的距离公式,求得$d=\frac{{|8k+2k(4{k^2}-1)-4k|}}{{\sqrt{16{k^2}+{{(4{k^2}-1)}^2}}}}$=|BE|,则点B关于直线EF的对称点在直线MF上.
解答 解:(Ⅰ)由题意得2b=2$\sqrt{3}$,则b=$\sqrt{3}$,c=1,则a2=b2+c2=4,则a=2,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)证明:“点B关于直线EF的对称点在直线MF上”等价于“EF平分∠MFB”.
设直线AM的方程为y=k(x+2)(k≠0),则N(2,4k),E(2,2k).…(7分)
设点M(x0,y0),由$\left\{\begin{array}{l}{y=k(x+2)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,整理得(4k2+3)x2+16k2x+16k2-12=0,
由韦达定理可知-2x0=$\frac{16{k}^{2}-12}{3+4{k}^{2}}$,则x0=$\frac{-8{k}^{2}+6}{3+4{k}^{2}}$,y0=k(x0+2)=$\frac{12k}{3+4{k}^{2}}$,
①当MF⊥x轴时,x0=1,此时k=±$\frac{1}{2}$.
则M(1,±$\frac{3}{2}$),N(2,±2),E(2,±1).
此时,点E在∠BFM的角平分线所在的直线y=x-1或y=-x+1,
即EF平分∠MFB. …(10分)
②当k≠$\frac{1}{2}$时,直线MF的斜率为kMF=$\frac{{y}_{0}}{{x}_{0}-1}$=$\frac{4k}{1-4{k}^{2}}$,
所以直线MF的方程为4kx+(4k2-1)y-4k=0. …(11分)
所以点E到直线MF的距离$d=\frac{{|8k+2k(4{k^2}-1)-4k|}}{{\sqrt{16{k^2}+{{(4{k^2}-1)}^2}}}}$=$\frac{{|4k+2k(4{k^2}-1)|}}{{\sqrt{{{(4{k^2}+1)}^2}}}}$=$\frac{{|2k(4{k^2}+1)|}}{{|4{k^2}+1|}}$=|2k|=|BE|.
即点B关于直线EF的对称点在直线MF上,
综上可知:点B关于直线EF的对称点在直线MF上. …(14分)
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,点到直线的距离公式,考查分类讨论思想,属于中档题.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案| A. | {x|x≤-2或x≥2} | B. | {x|x<-2或x>2} | C. | {x|-2<x<2} | D. | {x|-2≤x≤2} |
| A. | 2x>2y | B. | lgx>lgy | C. | $\frac{1}{x}>\frac{1}{y}$ | D. | x2>y2 |
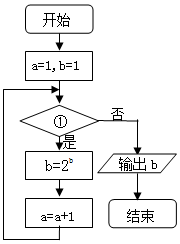
| A. | a>3? | B. | a≥3? | C. | a≤3? | D. | a<3? |
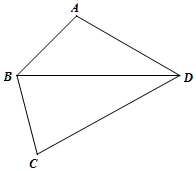 如图,在四边形ABCD中,∠ABD=45°,∠ADB=30°,BC=1,DC=2,cos∠BCD=$\frac{1}{4}$,则BD=2;三角形ABD的面积为$\sqrt{3}$-1.
如图,在四边形ABCD中,∠ABD=45°,∠ADB=30°,BC=1,DC=2,cos∠BCD=$\frac{1}{4}$,则BD=2;三角形ABD的面积为$\sqrt{3}$-1.