题目内容
13.圆(x-3)2+(y-3)2=4上到直线3x+4y-16=0的距离等于1的点有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 确定圆心和半径,求出圆心到直线的距离,与半径比较,数形结合可知共有三个交点.
解答 解:(x-3)2+(y-3)2=4是一个以(3,3)为圆心,2为半径的圆.
圆心到3x+4y-16=0的距离为d=$\frac{|9+12-16|}{5}$=1,
所以作与直线3x+4y-16=0距离为1的直线,
会发现这样的直线有两条(一条在直线的上方,一条在直线的下方),
上面的那条直线与圆有两个交点,下面的与圆有一个交点,
所以圆上共有三个点与直线距离为1.
故选C.
点评 本题考查了直线与圆的位置关系,用到点到直线的距离公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
8.设(1+3i)(2a+i)的实部与虚部相等,其中a为实数,则a=( )
| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
5.已知x,y 的取值如表所示,从散点图分析,y与x线性相关,且$\stackrel{∧}{y}$=0.85x+a,则a=( )
| x | 0 | 1 | 3 | 4 |
| y | 0.9 | 1.9 | 3.2 | 4.4 |
| A. | 1.5 | B. | 1.2 | C. | 0.9 | D. | 0.8 |
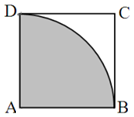 已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.
已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.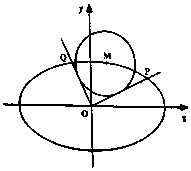 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,过点(0,-b),(a,0)的直线与原点的距离为$\sqrt{2}$,M(x0,y0)是椭圆上任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,过点(0,-b),(a,0)的直线与原点的距离为$\sqrt{2}$,M(x0,y0)是椭圆上任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.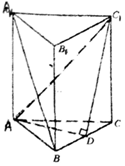 正三棱柱ABC-A1B1C1,BC=BB1=1,D为BC上一点,且满足AD⊥C1D.
正三棱柱ABC-A1B1C1,BC=BB1=1,D为BC上一点,且满足AD⊥C1D.