题目内容
10.已知△ABC的内角A,B,C的对边分别为a,b,c,若cosA=$\frac{1}{3}$,c=3b,且△ABC面积S△ABC=$\sqrt{2}$.(1)求边b.c;
(2)求边a并判断△ABC的形状.
分析 (1)由已知利用同角三角函数基本关系式可求sinA,利用三角形面积公式可求bc的值,又c=3b,即可解得b,c的值.
(2)由余弦定理可求a的值,由勾股定理即可得解△ABC为直角三角形.
解答 (本小题满分12分)
解:(1)∵cos A=$\frac{1}{3}$,
∴sin A=$\frac{2\sqrt{2}}{3}$.--------------(2分)
又S△ABC=$\frac{1}{2}$bcsin A=$\sqrt{2}$,
∴bc=3.----------------(4分)
又c=3b,
∴b=1,c=3.-----------------------------------------(6分)
(2)由余弦定理a2=b2+c2-2bccosA,-----(8分)
得:a2=1+9-2×$3×\frac{1}{3}$=8,
故a=2$\sqrt{2}$.-----(10分)
由c2=a2+b2知△ABC为直角三角形.-----------(12分)
点评 本题主要考查了同角三角函数基本关系式,三角形面积公式,余弦定理,勾股定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知x,y 的取值如表所示,从散点图分析,y与x线性相关,且$\stackrel{∧}{y}$=0.85x+a,则a=( )
| x | 0 | 1 | 3 | 4 |
| y | 0.9 | 1.9 | 3.2 | 4.4 |
| A. | 1.5 | B. | 1.2 | C. | 0.9 | D. | 0.8 |
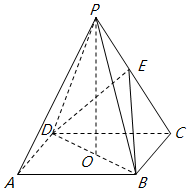 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证: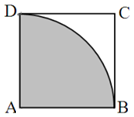 已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.
已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.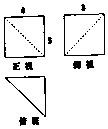 某几何体的三视图(单位:cm)如图所示,则此几何体的所有棱长之和为27+$\sqrt{34}$+$\sqrt{41}$cm,体积为20cm3.
某几何体的三视图(单位:cm)如图所示,则此几何体的所有棱长之和为27+$\sqrt{34}$+$\sqrt{41}$cm,体积为20cm3.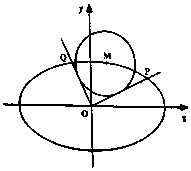 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,过点(0,-b),(a,0)的直线与原点的距离为$\sqrt{2}$,M(x0,y0)是椭圆上任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,过点(0,-b),(a,0)的直线与原点的距离为$\sqrt{2}$,M(x0,y0)是椭圆上任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.