题目内容
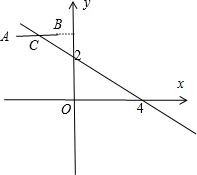
在直角坐标系xoy中线段AB与y轴垂直,其长度为2,AB的中点C在直线x+2y-4=0上,则∠AOB的最大值为______.
如图所示.
由题意可设A(a,b),B(2+a,b),则线段AB的中点C(a+1,b).
∵AB的中点C在直线x+2y-4=0上,∴a+1+2b-4=0,化为a+2b=3.
①当a=0时,b=
.此时A(0,
),B(2,
).
可得tan∠AOB=
=
=
.
②当a=-2时,b=
.此时A(-2,
),B(0,
).
可得tan∠AOB=
=
=
.
③当b=0时,a=3.此时A(3,0),B(5,0).
可得tan∠AOB=0.
④当a≠0,-2且b≠0时,此时kOA=
,kOB=
.
当b>0时,可得tan∠AOB=
=
=
=
=
.
tan∠AOB≤
=
=
,当且仅当b=
,a=3-2
时取等号.
当b<0时,tan∠AOB=
≤
.
综上可知:只有当a=3-2
时,b=
.可得tan∠AOB的最大值
.
故答案为:arctan
.
由题意可设A(a,b),B(2+a,b),则线段AB的中点C(a+1,b).
∵AB的中点C在直线x+2y-4=0上,∴a+1+2b-4=0,化为a+2b=3.
①当a=0时,b=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
可得tan∠AOB=
| |AB| |
| |OA| |
| 2 | ||
|
| 4 |
| 3 |
②当a=-2时,b=
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
可得tan∠AOB=
| |AB| |
| |OA| |
| 2 | ||
|
| 4 |
| 5 |
③当b=0时,a=3.此时A(3,0),B(5,0).
可得tan∠AOB=0.
④当a≠0,-2且b≠0时,此时kOA=
| b |
| a |
| b |
| 2+a |
当b>0时,可得tan∠AOB=
| kOA-kOB |
| 1+kOA•kOB |
| ||||
1+
|
| 2b |
| a(2+a)+b2 |
| 2b |
| (3-2b)(5-2b)+b2 |
| 2 | ||
5b+
|
tan∠AOB≤
| 2 | ||||
2
|
| 1 | ||
5
|
5
| ||
| 11 |
| 3 |
| 3 |
当b<0时,tan∠AOB=
| 2 | ||
16-5b-
|
| 1 | ||
8+5
|
综上可知:只有当a=3-2
| 3 |
| 3 |
5
| ||
| 11 |
故答案为:arctan
5
| ||
| 11 |


练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
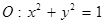 和点
和点 .
. 截得的弦长为8的圆M的方程;
截得的弦长为8的圆M的方程; 为定值?若存在,请求出定点R的坐标,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请求出定点R的坐标,并指出相应的定值;若不存在,请说明理由.