题目内容
已知圆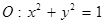 和点
和点 .
.
(1)过点M向圆O引切线,求切线的方程;
(2)求以点M为圆心,且被直线 截得的弦长为8的圆M的方程;
截得的弦长为8的圆M的方程;
(3)设P为(2)中圆M上任意一点,过点P向圆O引切线,切点为Q,试探究:平面内是否存在一定点R,使得 为定值?若存在,请求出定点R的坐标,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请求出定点R的坐标,并指出相应的定值;若不存在,请说明理由.
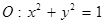 和点
和点 .
.(1)过点M向圆O引切线,求切线的方程;
(2)求以点M为圆心,且被直线
 截得的弦长为8的圆M的方程;
截得的弦长为8的圆M的方程;(3)设P为(2)中圆M上任意一点,过点P向圆O引切线,切点为Q,试探究:平面内是否存在一定点R,使得
 为定值?若存在,请求出定点R的坐标,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请求出定点R的坐标,并指出相应的定值;若不存在,请说明理由.(1): 或
或
(2)
(3)存在定点R ,此时
,此时 为定值
为定值 或定点R
或定点R ,此时
,此时 为定值
为定值
 或
或
(2)

(3)存在定点R
 ,此时
,此时 为定值
为定值 或定点R
或定点R ,此时
,此时 为定值
为定值
(1)若过点M的直线斜率不存在,直线方程为:
 ,为圆O的切线; 1分
,为圆O的切线; 1分当切线l的斜率存在时,设直线方程为:
 ,即
,即 ,
,∴圆心O到切线的距离为:
 ,解得:
,解得:
∴直线方程为:
 .
. 综上,切线的方程为:
 或
或 4分
4分(2)点
 到直线
到直线 的距离为:
的距离为: ,
,又∵圆被直线
 截得的弦长为8 ∴
截得的弦长为8 ∴ 7分
7分∴圆M的方程为:
 8分
8分(3)假设存在定点R,使得
 为定值,设
为定值,设 ,
, ,
,
∵点P在圆M上 ∴
 ,则
,则 10分
10分∵PQ为圆O的切线∴
 ∴
∴ ,
,

即

整理得:
 (*)
(*)若使(*)对任意
 恒成立,则
恒成立,则 13分
13分∴
 ,代入得:
,代入得:
整理得:
 ,解得:
,解得: 或
或 ∴
∴ 或
或
∴存在定点R
 ,此时
,此时 为定值
为定值 或定点R
或定点R ,此时
,此时 为定值
为定值 . 16分
. 16分
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
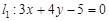 ,圆
,圆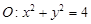 .
.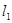 被圆
被圆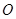 所截得的弦长;
所截得的弦长;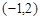 的直线
的直线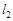 与直线
与直线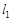 垂直,
垂直,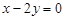 上的圆
上的圆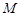 相切,圆
相切,圆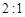 ,求圆
,求圆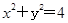 ,过点M(2,4)作圆C的两条切线,切点分别为A,B,
,过点M(2,4)作圆C的两条切线,切点分别为A,B,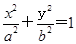 (a>b>0)的右顶点和上顶点.
(a>b>0)的右顶点和上顶点.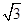 (k>0)与椭圆T相交于P,Q两点,O为坐标原点,
(k>0)与椭圆T相交于P,Q两点,O为坐标原点, +
+ ≤1
≤1