题目内容

10．下列命题中正确的是（　　）
A．经过不同的三点确定一个平面B．一点和一条直线确定一个平面
C．四边形一定是平面图形D．梯形一定是平面图形

分析 利用公理三及推论求解．

解答 解：经过不共线的三点确定一个平面，故A错误；
直线与直线外一点确定一个平面，故B错误；
四边形有可能是空间四边形，故C错误；
因为梯形中有一组对边平行，故梯形一定是平面图形，故D正确．
故选：D．

点评 本题考查命题真假的判断，是基础题，解题时要认真审题，注意公理三及推论的合理运用．

练习册系列答案
相关题目
2．在[-2π，2π]内，与α=-$\frac{11π}{3}$的终边相同的角为$\frac{π}{3}$．
1．已知数列{an}中，a1=2，前n项和为Sn，对于任意n∈N*，且n≥2，3Sn-4，an，2-$\frac{3}{2}$Sn-1总成等差数列．
（1）求数列{an}的通项公式an；
（2）若数列{bn}满足bn=3Sn，求数列{bn}的前n项和列Tn．
18．y=x-$\sqrt{1-4x}$的值域是{y|y≤$\frac{1}{4}$}．
5．已知函数$f（x）=\sqrt{3}sin2x+2{sin^2}x$．
（1）求$f（\frac{π}{12}）$的值；
（2）当$x∈[0，\frac{π}{2}]$时，求函数f（x）的值域．
15．如图程序执行完的结果是（　　）
A．5，-1B．4，-6C．1，-3D．无正确答案
2．已知A、B、C是直线l上的不同的三点，O是直线外一点，设$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$．
（1）证明：A、B、C三点共线的条件是λ+μ=1
（2）若$\overrightarrow{OA}=（3x+1）•\overrightarrow{OB}+（\frac{3}{2+3x}-y）•\overrightarrow{OC}$成立．记y=f（x），求函数y=f（x）的解析式；
（3）在（2）的条件下，若对任意x∈[$\frac{1}{6}$，$\frac{1}{3}$]，不等式|a-lnx|-ln[f（x）-3x]＞0恒成立，求实数a的取值范围．
19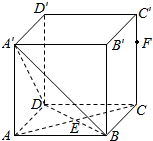．如图，正方体ABCD-A′B′C′D′中，$\overrightarrow{BD}=2\overrightarrow{BE}$．设点F在线段CC'上，直线EF与平面A'BD所成的角为α，则sinα的取值范围是（　　）
A．$[\frac{{\sqrt{3}}}{3}，1]$B．$[\frac{{2\sqrt{2}}}{3}，1]$C．$[\frac{{\sqrt{6}}}{3}，\frac{{2\sqrt{2}}}{3}]$D．$[\frac{{\sqrt{6}}}{3}，1]$
20．实数x，y满足x≥1，y≥1，且（logax）2+（logay）2=loga（ax2）+loga（ay2）（0＜a＜1），则loga（xy）的取值范围是（　　）
A．[2-2$\sqrt{2}$，2+2$\sqrt{2}$]B．[2-2$\sqrt{2}$，1-$\sqrt{3}$]
C．[1+$\sqrt{3}$，2+2$\sqrt{2}$]D．[2-2$\sqrt{2}$，1-$\sqrt{3}$]∪[1+$\sqrt{3}$，2+2$\sqrt{2}$]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网