题目内容
13.已知函数f(x)=-x2+3x•|x-a|,其中a>0.(1)当a=2时,求函数在x∈(-1,6)上的值域;
(2)若函数在x∈(-1,6)上既有最大值又有最小值,求a的范围.
分析 (1)当a=2时,f(x)=-x2+3x•|x-2|=$\left\{\begin{array}{l}{-4{x}^{2}+6x,x∈(-1,2]}\\{2{x}^{2}-6x,x∈(2,6)}\end{array}\right.$,从而确定函数的单调性,从而求值域;
(2)由(1)知,0<a<6,化简f(x)=-x2+3x•|x-a|=$\left\{\begin{array}{l}{-4{x}^{2}+3ax,x∈(-1,a]}\\{2{x}^{2}-3ax,x∈(a,6)}\end{array}\right.$;从而确定函数的单调性,从而可得$\left\{\begin{array}{l}{-{a}^{2}≤-4-3a}\\{\frac{9{a}^{2}}{16}≥72-18a}\end{array}\right.$,从而解得.
解答 解:(1)当a=2时,
f(x)=-x2+3x•|x-2|=$\left\{\begin{array}{l}{-4{x}^{2}+6x,x∈(-1,2]}\\{2{x}^{2}-6x,x∈(2,6)}\end{array}\right.$,
由二次函数的性质可知,
f(x)在(-1,$\frac{3}{4}$)上是增函数,在[$\frac{3}{4}$,2)上是减函数,
在[2,6)上是增函数;
而f(-1)=-4-6=-10,f($\frac{3}{4}$)=$\frac{9}{4}$,f(2)=-4,f(6)=36;
故函数在(-1,6)上的值域为(-10,36);
(2)由(1)知,0<a<6,
f(x)=-x2+3x•|x-a|=$\left\{\begin{array}{l}{-4{x}^{2}+3ax,x∈(-1,a]}\\{2{x}^{2}-3ax,x∈(a,6)}\end{array}\right.$;
由二次函数的性质可知,
f(x)在(-1,$\frac{3a}{8}$)上是增函数,在[$\frac{3a}{8}$,a)上是减函数,
在[a,6)上是增函数;
其中f(-1)=-4-3a,f($\frac{3a}{8}$)=$\frac{9{a}^{2}}{16}$,f(a)=-a2,f(6)=72-18a;
故若函数在x∈(-1,6)上既有最大值又有最小值,
则$\left\{\begin{array}{l}{-{a}^{2}≤-4-3a}\\{\frac{9{a}^{2}}{16}≥72-18a}\end{array}\right.$,
解得,4≤a<6.
点评 本题考查了绝对值函数的应用及分段函数的应用,同时考查了分类讨论的思想应用.

| A. | c2=a2+b2+2abcosC | B. | c2=a2+b2-2abcosC | ||
| C. | c2=a2+b2+2absinC | D. | c2=a2+b2-2absinC |
| A. | 13 | B. | 15 | C. | 17 | D. | 48 |
(2)函数$g(x)=\frac{2}{x}+lnx+x-2-b(b∈R)$.在区间[e-1,e]上有两个零点,求实数b的取值范围;
(3)完成填空
| 用方程表述 | 用函数零点表述 | |
| 若函数y=f(x)和y=g(x)的图象在(a,b)内有交点 |
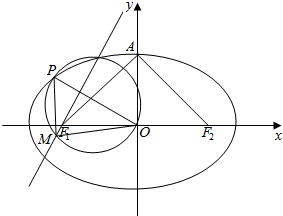 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,点A是椭圆的上顶点,△AF1F2为等腰直角三角形,点P为椭圆任意一点,且|PF1|的最小值为$\sqrt{2}$-1;以OP为直径作圆E,过F1作OP的垂线交圆E于M.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,点A是椭圆的上顶点,△AF1F2为等腰直角三角形,点P为椭圆任意一点,且|PF1|的最小值为$\sqrt{2}$-1;以OP为直径作圆E,过F1作OP的垂线交圆E于M.