题目内容
已知函数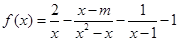
(Ⅰ)若函数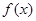 无零点,求实数
无零点,求实数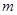 的取值范围;
的取值范围;
(Ⅱ)若函数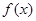 在
在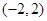 有且仅有一个零点,求实数
有且仅有一个零点,求实数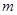 的取值范围.
的取值范围.
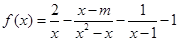
(Ⅰ)若函数
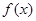 无零点,求实数
无零点,求实数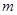 的取值范围;
的取值范围;(Ⅱ)若函数
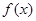 在
在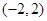 有且仅有一个零点,求实数
有且仅有一个零点,求实数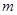 的取值范围.
的取值范围.(Ⅰ)  或
或 ;(Ⅱ)
;(Ⅱ) 或
或 。
。
 或
或 ;(Ⅱ)
;(Ⅱ) 或
或 。
。试题分析:(Ⅰ) 函数
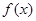 无零点,即
无零点,即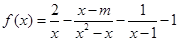 =0,也就是
=0,也就是 无解,
无解, 无解或x=0,1是其根。
无解或x=0,1是其根。所以
 ,或m-2=0,或-1+1+m-2=0,
,或m-2=0,或-1+1+m-2=0,即
 或
或 ; ……6分
; ……6分(Ⅱ) 函数
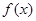 在
在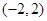 有且仅有一个零点,所以
有且仅有一个零点,所以 或
或 ,或有一根为
,或有一根为 2,另一根在(-2,2)解得,
2,另一根在(-2,2)解得, 或
或 …… 12分
…… 12分点评:易错题,解答本题关键 是利用转化与化归思想,将分式函数的零点问题转化成为一元二次方程根的讨论问题。其中(II)小题,易忽视有一根为
 2,另一根在(-2,2)的情况而出错。考虑问题要全面。
2,另一根在(-2,2)的情况而出错。考虑问题要全面。
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 ,其中
,其中 为常数,且
为常数,且 .若
.若 为常数,则
为常数,则 的值__________
的值__________ 的零点属于区间
的零点属于区间 ,则
,则 .
. ,若对
,若对 ,使得
,使得 ,则实数
,则实数 的取值范围是 .
的取值范围是 .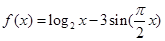 零点的个数是 ( )
零点的个数是 ( ) 则
则 ( )
( ) 内均有零点
内均有零点 内无零点,在区间
内无零点,在区间 内有零点
内有零点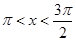 ,则方程
,则方程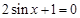 的解
的解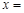 .
.  ,曲线
,曲线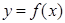 在点
在点 处的切线方程为
处的切线方程为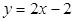 .
.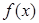 的解析式;
的解析式;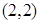 能作几条直线与曲线
能作几条直线与曲线 在区间[-1 , 2 ]上有两个不同的
在区间[-1 , 2 ]上有两个不同的 的取值范围是 ;
的取值范围是 ;