题目内容
(本小题满分12分)
已知函数 ,曲线
,曲线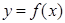 在点
在点 处的切线方程为
处的切线方程为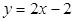 .
.
(1)求函数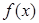 的解析式;
的解析式;
(2)过点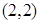 能作几条直线与曲线
能作几条直线与曲线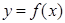 相切?说明理由.
相切?说明理由.
已知函数
 ,曲线
,曲线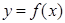 在点
在点 处的切线方程为
处的切线方程为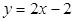 .
.(1)求函数
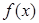 的解析式;
的解析式;(2)过点
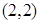 能作几条直线与曲线
能作几条直线与曲线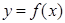 相切?说明理由.
相切?说明理由.(1)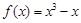 (2)三条切线
(2)三条切线
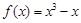 (2)三条切线
(2)三条切线试题分析:(1)
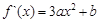 ,由题知…………………………………………………(1分)
,由题知…………………………………………………(1分)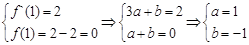
∴
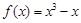 …………………………………………………………………………(5分)
…………………………………………………………………………(5分)(2)设过点(2,2)的直线与曲线
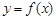 相切于点
相切于点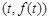 ,则切线方程为:
,则切线方程为: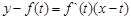
即
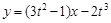 ……………………………………………………………………(7分)
……………………………………………………………………(7分)由切线过点(2,2)得:
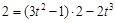
过点(2,2)可作曲线
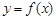 的切线条数就是方程
的切线条数就是方程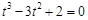 的实根个数……(9分)
的实根个数……(9分)令
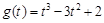 ,则
,则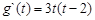
由
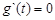 得
得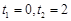
当t变化时,
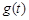 、
、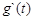 的变化如下表
的变化如下表| t | 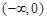 | 0 | (0,2) | 2 | 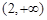 |
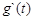 | + | 0 | - | 0 | + |
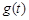 | ↗ | 极大值2 | ↘ | 极小值-2 | ↗ |
 知,故
知,故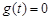 有三个不同实根可作三条切线………………(12分)
有三个不同实根可作三条切线………………(12分)点评:导数的几何意义:函数在某一点处的导数值等于该点处的切线斜率,第二问求切线条数准化为求切点个数,进而化为求方程的根,此时可与函数最值结合,此题出的比较巧妙

练习册系列答案
相关题目
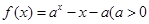 且
且 有两个零点,则实数
有两个零点,则实数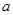 的取值范围是 .
的取值范围是 .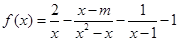
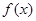 无零点,求实数
无零点,求实数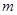 的取值范围;
的取值范围;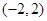 有且仅有一个零点,求实数
有且仅有一个零点,求实数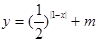 存在零点,则m的取值范围是__________.
存在零点,则m的取值范围是__________. ]上的零点个数为
]上的零点个数为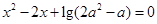 有一个正根和一个负根,则实数
有一个正根和一个负根,则实数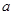 的取值范围是_________________.
的取值范围是_________________. 的定义域为开区间
的定义域为开区间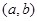 ,导函数
,导函数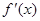 在
在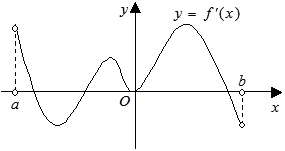
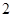 个
个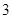 个
个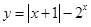 零点的个数为( )
零点的个数为( ) 的解可视为函数
的解可视为函数 的图像与函数
的图像与函数 的图像交点的横坐标.若方程
的图像交点的横坐标.若方程 的各个实根
的各个实根 所对应的点
所对应的点 (
( =1,2,…,k)均在直线
=1,2,…,k)均在直线 的同侧(不包括在直线上),则实数
的同侧(不包括在直线上),则实数 的取值范围是______.
的取值范围是______.