题目内容
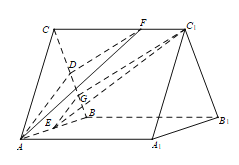
【题目】如图，在直三棱柱
中，
，
分别是棱
，
的中点，点
在
棱上，且
，
，
.
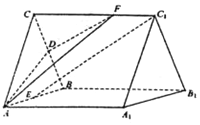
（1）求证：
平面
；
（2）当
时，求三棱锥
的体积.
【答案】（1）见解析；（2）
【解析】试题分析：（1）连接
交
于点
，由重心性质可得
，由相似可得
，最后根据线面平行判定定理得结论（2）取
上一点
使
，利用平行进行等体积代换
，最后根据锥体体积公式求体积
试题解析：解：（1）(法一)连接交于点，连接
由
分别是棱
中点，故点为
的重心
在
中，有
，又
平面
平面
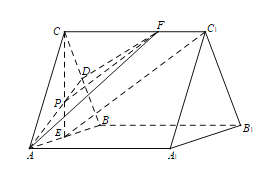
（法二）取
的中点
，连接
由
是棱
的中点，为的中点，
为的中位线，即
平面
又
为棱
的中点，为的中点
由
，由
，且
为直三棱柱
，进而得
，即
平面
又
平面
平面
又
平面
平面
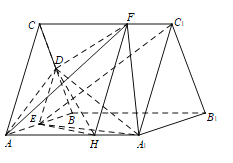
(2)取上一点使
∵
且直三棱柱
∴
，∵为中点
∴
,
,
平面
∴
而
,
点到平面
的距离等于
∴
∴三棱锥
的体积为
练习册系列答案
习题精选系列答案
相关题目
