题目内容
若关于x的方程
=kx有三个不同的实根,则实数k的取值范围是 .
| |x| |
| x+2 |
考点:根的存在性及根的个数判断
专题:计算题,函数的性质及应用
分析:化简方程,讨论去掉绝对值号.
解答:
解:方程可化为|x|=kx(x+2)(x≠-2),
由题意,k≠0,
当x≥0时,原方程可化为x=kx(x+2),
解得,x=0,或x=-2+
,
当x<0时,原方程可化为-x=kx(x+2),
解得,x=-2-
,
∵关于x的方程
=kx有三个不同的实根,
∴-2+
>0且-2-
<0,
解得,0<k<
.
故答案为:0<k<
.
由题意,k≠0,
当x≥0时,原方程可化为x=kx(x+2),
解得,x=0,或x=-2+
| 1 |
| k |
当x<0时,原方程可化为-x=kx(x+2),
解得,x=-2-
| 1 |
| k |
∵关于x的方程
| |x| |
| x+2 |
∴-2+
| 1 |
| k |
| 1 |
| k |
解得,0<k<
| 1 |
| 2 |
故答案为:0<k<
| 1 |
| 2 |
点评:本题考查了绝对值方程的解决方法,注意讨论.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
若两个等差数列{an}、{bn}的前项和分别为Sn、Tn,对任意的n∈N*都有
=
,则
+
的值是( )
| Sn |
| Tn |
| 2n-1 |
| 4n-3 |
| a4 |
| b5+b8 |
| a9 |
| b3+b10 |
A、
| ||
B、
| ||
C、
| ||
D、
|
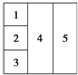 如图,用4种不同的颜色对图中5个区域涂色( 4种颜色全部使用 ),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色方法有
如图,用4种不同的颜色对图中5个区域涂色( 4种颜色全部使用 ),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色方法有