题目内容
设F1，F2为双曲线
的左右焦点，P为双曲线右支上任一点，当
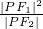最小值为8a时，该双曲线离心率e的取值范围是________．
（1，3]
分析：由定义知：|PF2|-|PF1|=2a，∴|PF2|=2a+|PF1|，∴
=
．
当且仅当
，即||PF1|=2a时取得等号．然后利用焦半径公式可以导出该双曲线离心率e的取值范围．
解答：由定义知：|PF2|-|PF1|=2a，
∴|PF2|=2a+|PF1|，
∴=．
当且仅当，即||PF1|=2a时取得等号．
设P（x0，y0），（x0≤-a）
依焦半径公式得：|PF1|=-e×x0-a=2a，
∴
又∵e＞1，故e∈（1，3]
答案：（1，3]．
点评：本题考查双曲线的定义、焦半径、离心率、均值不等式，解题时要注意公式的合理选用．
分析：由定义知：|PF2|-|PF1|=2a，∴|PF2|=2a+|PF1|，∴
=．当且仅当
，即||PF1|=2a时取得等号．然后利用焦半径公式可以导出该双曲线离心率e的取值范围．解答：由定义知：|PF2|-|PF1|=2a，
∴|PF2|=2a+|PF1|，
∴
=．当且仅当
，即||PF1|=2a时取得等号．设P（x0，y0），（x0≤-a）
依焦半径公式得：|PF1|=-e×x0-a=2a，
∴
又∵e＞1，故e∈（1，3]
答案：（1，3]．
点评：本题考查双曲线的定义、焦半径、离心率、均值不等式，解题时要注意公式的合理选用．
练习册系列答案
考前必练系列答案
相关题目