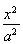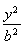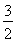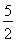Question

设F₁和F₂为双曲线

x2

a2

-

y2

b2

=1(a＞0，b＞0)的两个焦点，若F₁、F₂、P（0，2b）是正三角形的三个顶点，则双曲线的离心率为

2

．

Answer 1

分析：设F₁（-c，0），F₂（c，0），则|F₁P|=

c2+4b2

，由F₁、F₂、P（0，2b）是正三角形的三个顶点可知

c2+4b2

=2c，由此可求出双曲线的离心率．

解答：解：设F₁（-c，0），F₂（c，0），则|F₁P|=

c2+4b2

，
∵F₁、F₂、P（0，2b）是正三角形的三个顶点，
∴

c2+4b2

=2c，∴c²+4b²=4c²，
∴c²+4（c²-a²）=4c²，
∴c²=4a²，
∴e²=4，
∴e=2．
答案：2．

点评：本题考查双曲线的性质，在解题时要注意审题，由F₁、F₂、P（0，2b）是正三角形的三个顶点建立方程．