题目内容
如图,等边三角形 的中线
的中线 与中位线
与中位线 相交于
相交于 ,已知
,已知 是△
是△ 绕
绕 旋转过程中的一个图形,下列命题中,错误的是( )
旋转过程中的一个图形,下列命题中,错误的是( )

 的中线
的中线 与中位线
与中位线 相交于
相交于 ,已知
,已知 是△
是△ 绕
绕 旋转过程中的一个图形,下列命题中,错误的是( )
旋转过程中的一个图形,下列命题中,错误的是( ) A.动点 在平面 在平面 上的射影在线段 上的射影在线段 上 上 |
B.恒有平面 ⊥平面 ⊥平面 |
C.三棱锥 的体积有最大值 的体积有最大值 |
D.异面直线 与 与 不可能垂直 不可能垂直 |

D
试题分析:由于
 .所以
.所以 平面
平面 .经过点
.经过点 作平面ABC的垂线垂足在AF上.所以A选项正确.由A可知B选项正确.当平面
作平面ABC的垂线垂足在AF上.所以A选项正确.由A可知B选项正确.当平面 垂直于平面
垂直于平面 时,三棱锥
时,三棱锥 的体积最大,所以C正确.因为
的体积最大,所以C正确.因为 ,设
,设 .所以
.所以 ,当
,当 时,
时, .所以异面直线
.所以异面直线 与
与 可能垂直.所以D选项不正确.
可能垂直.所以D选项不正确.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
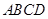 中,
中,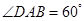 ,
,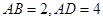 ,将
,将 沿
沿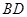 折起到
折起到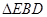 的位置.
的位置. 平面
平面 ;
;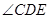 取何值时,三棱锥
取何值时,三棱锥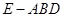 的体积取最大值?并求此时三棱锥
的体积取最大值?并求此时三棱锥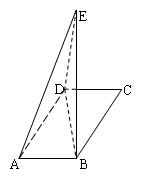

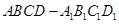 中,底面
中,底面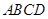 是边长为
是边长为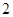 的正方形,
的正方形,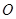 为
为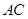 与
与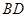 的交点,
的交点,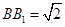 ,
,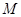 是线段
是线段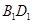 的中点.
的中点.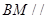 平面
平面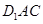 ;
;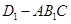 的体积.
的体积.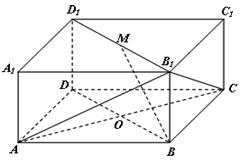
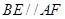 ,
,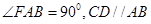 ,讲DCEF沿CD折起,使得
,讲DCEF沿CD折起,使得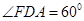 ,得到一个几何体,
,得到一个几何体,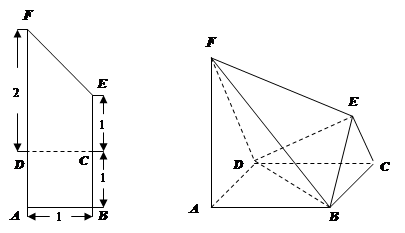
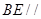 平面ADF;
平面ADF;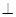 平面ABCD;
平面ABCD;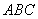 中,
中, 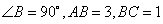 ,以边
,以边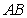 所在直线为旋转轴,其余各边旋转一周而形成的曲面所围成的几何体的体积为( )
所在直线为旋转轴,其余各边旋转一周而形成的曲面所围成的几何体的体积为( )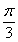
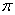
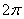
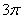
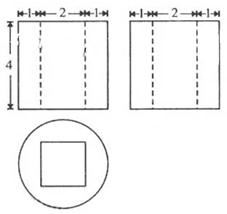
 及其内部一动点
及其内部一动点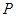 ,集合
,集合 ,则集合
,则集合 构成的几何体表面积为 .
构成的几何体表面积为 .