题目内容
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,且AC=AD=CD=DE=2,AB=1.

(1)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一结论;
(2)求多面体ABCDE的体积.

(1)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一结论;
(2)求多面体ABCDE的体积.
(1)见解析 (2)

(1)如图所示,由已知AB⊥平面ACD,DE⊥平面ACD,∴AB∥ED,

设F为线段CE的中点,H是线段CD的中点,连接BF、FH、AH,则FH= ED,又AB=
ED,又AB= ED,
ED,
∴FH=AB,
∴四边形ABFH是平行四边形,∴BF∥AH,
又因为BF?平面ACD,AH?平面ACD,
∴BF∥平面ACD.
(2)取AD中点G,连接CG.
因为AB⊥平面ACD,∴CG⊥AB,又CG⊥AD,
∴CG⊥平面ABED,即CG为四棱锥C—ABED的高,求得CG= ,
,
∴VC—ABED= ·
· ·2·
·2· =
= .
.

设F为线段CE的中点,H是线段CD的中点,连接BF、FH、AH,则FH=
 ED,又AB=
ED,又AB= ED,
ED,∴FH=AB,
∴四边形ABFH是平行四边形,∴BF∥AH,
又因为BF?平面ACD,AH?平面ACD,
∴BF∥平面ACD.
(2)取AD中点G,连接CG.
因为AB⊥平面ACD,∴CG⊥AB,又CG⊥AD,
∴CG⊥平面ABED,即CG为四棱锥C—ABED的高,求得CG=
 ,
,∴VC—ABED=
 ·
· ·2·
·2· =
= .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,平面
中,平面 平面
平面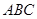 ,
, 于点
于点 ,且
,且 ,
, ,
, 

 ,
, ,求三棱锥
,求三棱锥
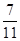
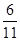
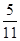
 , CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
, CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.  ,求
,求 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
 的中线
的中线 与中位线
与中位线 相交于
相交于 ,已知
,已知 是△
是△ 绕
绕 在平面
在平面 ⊥平面
⊥平面
 的体积有最大值
的体积有最大值 与
与 不可能垂直
不可能垂直
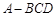 中,
中,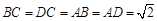 ,
,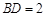 ,平面
,平面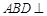 平面
平面 ,
,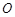 为
为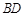 中点,点
中点,点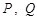 分别为线段
分别为线段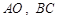 上的动点(不含端点),且
上的动点(不含端点),且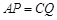 ,则三棱锥
,则三棱锥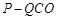 体积的最大值为________.
体积的最大值为________.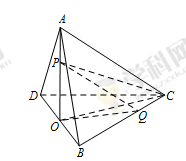

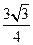
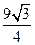
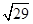 ,AC=BD=
,AC=BD=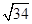 ,AD=BC=
,AD=BC=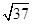 ,则四面体ABCD的外接球的表面积为( )
,则四面体ABCD的外接球的表面积为( )