题目内容
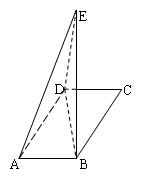
如图,在平行四边形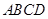 中,
中,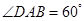 ,
,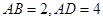 ,将
,将 沿
沿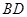 折起到
折起到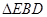 的位置.
的位置.
(1)求证: 平面
平面 ;
;
(2)当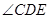 取何值时,三棱锥
取何值时,三棱锥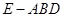 的体积取最大值?并求此时三棱锥
的体积取最大值?并求此时三棱锥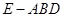 的侧面积.
的侧面积.
 中,
中,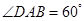 ,
,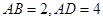 ,将
,将 沿
沿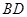 折起到
折起到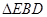 的位置.
的位置.(1)求证:
 平面
平面 ;
;(2)当
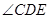 取何值时,三棱锥
取何值时,三棱锥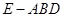 的体积取最大值?并求此时三棱锥
的体积取最大值?并求此时三棱锥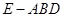 的侧面积.
的侧面积.
(1)证明过程详见解析;(2)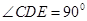 时,三棱锥
时,三棱锥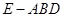 体积取最大值,此时侧面积
体积取最大值,此时侧面积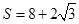 .
.
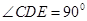 时,三棱锥
时,三棱锥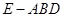 体积取最大值,此时侧面积
体积取最大值,此时侧面积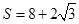 .
.试题分析:本题主要考查余弦定理、勾股定理、线面垂直、三角形面积公式、三棱锥的侧面积和体积等基础知识,考查学生的空间想象能力、逻辑推理能力.第一问,在
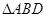 中,利用余弦定理得到BD的长,从而判断出
中,利用余弦定理得到BD的长,从而判断出 ,利用平行线,得
,利用平行线,得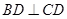 ,
,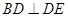 ,利用线面垂直的判定得
,利用线面垂直的判定得 平面
平面 ;
;第二问,结合第一问的证明知,当
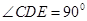 时,三棱锥的体积最大,此时
时,三棱锥的体积最大,此时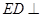 平面
平面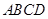 ,所以
,所以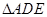 和
和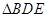 为直角三角形,由线面垂直的判定可证出
为直角三角形,由线面垂直的判定可证出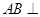 平面
平面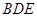 ,所以
,所以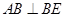 ,所以
,所以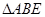 为直角三角形,所以三棱锥的侧面积为3个直角三角形之和.
为直角三角形,所以三棱锥的侧面积为3个直角三角形之和.试题解析:(I)在
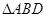 中,
中,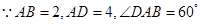
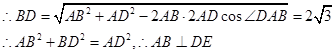
∵
 ∴
∴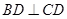 ,
,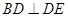
又

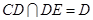 ,
, 、
、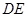
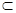 平面
平面
∴
 平面
平面
(2)设E点到平面ABCD距离为
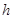 ,则
,则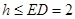 .
.由(I)知
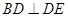
当
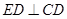 时,
时,∵
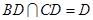 ,
, 、
、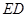
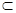 平面
平面
∴
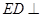 平面
平面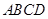
∴当
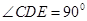 时,
时,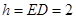 ,三棱锥
,三棱锥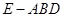 的体积取最大值.
的体积取最大值.此时
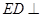 平面
平面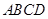 ,∴
,∴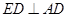 、
、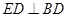
在
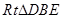 中,
中,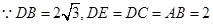
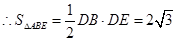
在Rt△ADE中,
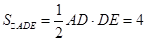
∵
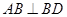 ,
,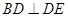 ,
,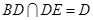 ,
,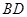 、
、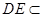 平面
平面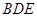
∴
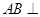 平面
平面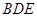 ∴
∴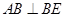
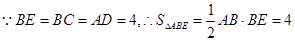
综上,
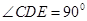 时,三棱锥
时,三棱锥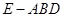 体积取最大值,此时侧面积
体积取最大值,此时侧面积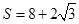 .
.
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
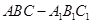 中,
中,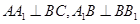 .
.
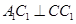 ;
;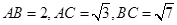 ,问
,问 为何值时,三棱柱
为何值时,三棱柱
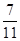
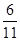
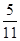
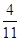
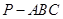 中,
中,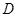 ,
,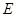 分别为
分别为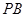 ,
,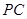 的中点,记三棱锥
的中点,记三棱锥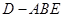 的体积为
的体积为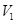 ,
,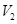 ,则
,则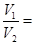 ________.
________. 的中线
的中线 与中位线
与中位线 相交于
相交于 ,已知
,已知 是△
是△ 绕
绕 在平面
在平面 ⊥平面
⊥平面
 的体积有最大值
的体积有最大值 与
与 不可能垂直
不可能垂直
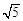 cm的圆面,球心到这个平面的距离是2cm,则球O的体积是( )
cm的圆面,球心到这个平面的距离是2cm,则球O的体积是( )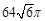 cm3
cm3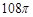 cm3
cm3