题目内容
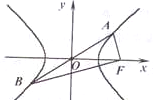 如图,已知双曲线
如图,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 12 |
| π |
| 6 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用S△ABF=2S△AOF,先求出e2=
,再根据α∈[
,
],即可求出双曲线离心率的取值范围.
| 1 |
| 1-sin2α |
| π |
| 12 |
| π |
| 6 |
解答:
解:设左焦点为F',令|AF|=r1,|AF'|=r2,则|BF|=|F'A|=r2,
∴r2-r1=2a,
∵点A关于原点O的对称点为B,AF⊥BF,
∴|OA|=|OB|=|OF|=c,
∴r22+r12═4c2,
∴r1r2=2(c2-a2)
∵S△ABF=2S△AOF,
∴
r1r2═2•
c2sin2α,
∴r1r2═2c2sin2α
∴c2sin2α=c2-a2
∴e2=
,
∵α∈[
,
],
∴sin2α∈[
,
],
∴e2=
∈[2,(
+1)2]
∴e∈[
,
+1].
故选:B.
∴r2-r1=2a,
∵点A关于原点O的对称点为B,AF⊥BF,
∴|OA|=|OB|=|OF|=c,
∴r22+r12═4c2,
∴r1r2=2(c2-a2)
∵S△ABF=2S△AOF,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴r1r2═2c2sin2α
∴c2sin2α=c2-a2
∴e2=
| 1 |
| 1-sin2α |
∵α∈[
| π |
| 12 |
| π |
| 6 |
∴sin2α∈[
| 1 |
| 2 |
| ||
| 2 |
∴e2=
| 1 |
| 1-sin2α |
| 3 |
∴e∈[
| 2 |
| 3 |
故选:B.
点评:本题考查双曲线的离心率的取值范围的求法,是中档题,解题时要认真审题,注意三角函数性质的灵活运用.

练习册系列答案
相关题目
等差数列{an}的公差d≠0,a1=20,且a3,a7,a9成等比数列.Sn为{an}的前n项和,则S10的值为( )
| A、-110 | B、-90 |
| C、90 | D、110 |