题目内容
已知函数f(x)=ex,g(x)=mx2+ax+b,其中m,a,b∈R,e=2.71828…为自然对数的底数.
(1)设函数h(x)=xf(x),当a=1,b=0时,若函数h(x)与g(x)具有相同的单调区间,求m的值;
(2)当m=0时,记F(x)=f(x)-g(x)
①当a=2时,若函数F(x)在[-1,2]上存在两个不同的零点,求b的取值范围;
②当b=-
时,试探究是否存在正整数a,使得函数F(x)的图象恒在x轴的上方?若存在,求出a的最大值;若不存在,请说明理由.
(1)设函数h(x)=xf(x),当a=1,b=0时,若函数h(x)与g(x)具有相同的单调区间,求m的值;
(2)当m=0时,记F(x)=f(x)-g(x)
①当a=2时,若函数F(x)在[-1,2]上存在两个不同的零点,求b的取值范围;
②当b=-
| 15 |
| 2 |
考点:函数零点的判定定理,二次函数的性质
专题:函数的性质及应用
分析:(1)求解导数得出:h(x)=xex,(-∞,-1)上单调递减,(-1,+∞)单调递增,x=-1时h(x)去极小值.
(2)①当m=0时,记F(x)=f(x)-g(x)=ex-ax-b,
F(x)在(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增,F(x)的最小值为F(ln2)=2-2ln2-b,根据函数性质得出:2-2ln2-b<0,F(-1)≥0,F(2)≥0,
②判断得出:当a=1时,F(x)=ex-x+
,F(x)在(0,+∞)单调递增,在(-∞,0)上单调递减,最小值为F(0)=1+
,>0,F(x)>0恒成立,
(2)①当m=0时,记F(x)=f(x)-g(x)=ex-ax-b,
F(x)在(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增,F(x)的最小值为F(ln2)=2-2ln2-b,根据函数性质得出:2-2ln2-b<0,F(-1)≥0,F(2)≥0,
②判断得出:当a=1时,F(x)=ex-x+
| ′15 |
| 2 |
| 15 |
| 2 |
解答:
解:(1)∵函数f(x)=ex,函数h(x)=xf(x),
∴h(x)=xex,
∴h′(x)=ex+xex,
∵h′(x)=ex+xex=0,x=-1,
h′(x)=ex+xex>0,x>-1,
h′(x)=ex+xex<0,x<-1,
∴h(x)=xex,(-∞,-1)上单调递减,(-1,+∞)单调递增,x=-1时h(x)去极小值,
∵当a=1,b=0时g(x)=mx2+ax+b=mx2+x,若函数h(x)与g(x)具有相同的单调区间
∴-12m=-1,m=12,
(2)当m=0时,记F(x)=f(x)-g(x)=ex-ax-b,
①当a=2时,F(x)=ex-2x-b,
∴F′(x)=ex-2,
∵F′(x)=ex-2=0,x=ln2,
F′(x)=ex-2>0,x>ln2
F′(x)=ex-2<0,x<ln2,
∴F(x)在(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增,
F(x)的最小值为F(ln2)=2-2ln2-b,
∵函数F(x)在[-1,2]上存在两个不同的零点,
∴2-2ln2-b<0,F(-1)≥0,F(2)≥0,
解得出:b>2-2ln2,b≤
+2,b≤e2-4,
即2-2ln2<b≤
+2,
②∵当b=-
时,F(x)=f(x)-g(x)=ex-ax+
,
∴F′(x)=ex-a,
当a=1时,F(x)=ex-x+
,
F′(x)=ex-1,
∵F′(x)=ex-1>0,x>0,
F′(x)=ex-1=0,x=0,
F′(x)=ex-1<0,x<0,
∴F(x)在(0,+∞)单调递增,在(-∞,0)上单调递减,
最小值为F(0)=1+
>0,∴F(x)>0恒成立,
当a=1时,使得函数F(x)的图象恒在x轴的上方.
∴h(x)=xex,
∴h′(x)=ex+xex,
∵h′(x)=ex+xex=0,x=-1,
h′(x)=ex+xex>0,x>-1,
h′(x)=ex+xex<0,x<-1,
∴h(x)=xex,(-∞,-1)上单调递减,(-1,+∞)单调递增,x=-1时h(x)去极小值,
∵当a=1,b=0时g(x)=mx2+ax+b=mx2+x,若函数h(x)与g(x)具有相同的单调区间
∴-12m=-1,m=12,
(2)当m=0时,记F(x)=f(x)-g(x)=ex-ax-b,
①当a=2时,F(x)=ex-2x-b,
∴F′(x)=ex-2,
∵F′(x)=ex-2=0,x=ln2,
F′(x)=ex-2>0,x>ln2
F′(x)=ex-2<0,x<ln2,
∴F(x)在(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增,
F(x)的最小值为F(ln2)=2-2ln2-b,
∵函数F(x)在[-1,2]上存在两个不同的零点,
∴2-2ln2-b<0,F(-1)≥0,F(2)≥0,
解得出:b>2-2ln2,b≤
| 1 |
| e |
即2-2ln2<b≤
| 1 |
| e |
②∵当b=-
| 15 |
| 2 |
| ′15 |
| 2 |
∴F′(x)=ex-a,
当a=1时,F(x)=ex-x+
| ′15 |
| 2 |
F′(x)=ex-1,
∵F′(x)=ex-1>0,x>0,
F′(x)=ex-1=0,x=0,
F′(x)=ex-1<0,x<0,
∴F(x)在(0,+∞)单调递增,在(-∞,0)上单调递减,
最小值为F(0)=1+
| 15 |
| 2 |
当a=1时,使得函数F(x)的图象恒在x轴的上方.
点评:本题考查了函数思想的运用,导数在求解单调性,最值中的应用,知识比较多,难度较大,属于难题.

练习册系列答案
相关题目
曲线y=xex+2x+1在点(0,1)处的切线方程为( )
| A、x+3y-3=0 |
| B、3x-y+1=0 |
| C、3x+y-1=0 |
| D、x-3y+3=0 |
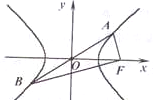 如图,已知双曲线
如图,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 12 |
| π |
| 6 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
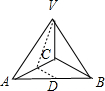 在三棱锥V-ABC中,D、E分别为AB,AC的中点,平面VCB⊥平面ABC,AC⊥BC.
在三棱锥V-ABC中,D、E分别为AB,AC的中点,平面VCB⊥平面ABC,AC⊥BC.