题目内容
13.若过点P(1-a,1+a)和Q(3,2a)的直线的倾斜角为钝角,则实数a的取值范围是( )| A. | (-2,1) | B. | (-1,2) | C. | (-∞,0) | D. | (-∞,-2)∪(1,+∞) |
分析 由直线的倾斜角α为钝角,能得出直线的斜率小于0,解不等式求出实数a的取值范围.
解答 解:∵过点P(1-a,1+a)和Q(3,2a)的直线的倾斜角α为钝角,
∴直线的斜率小于0,
即 $\frac{2a-a-1}{3-1+a}$<0,即 $\frac{a-1}{a+2}$<0,解得-2<a<1,
故选:A
点评 本题考查直线的斜率公式及直线的倾斜角与斜率的关系.

练习册系列答案
相关题目
1.复数z=$\frac{1+i}{i}$,则|z|=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | -$\sqrt{2}$ | D. | 1-i |
2.已知全集A={x|x≤9,x∈N*}集合B={x|0<x<7},则A∩B=( )
| A. | {x|0<x<7} | B. | {x|1≤x≤6} | C. | {1,2,3,4,5,6} | D. | {7,8,9} |
3.设圆O1和圆O2是两个定圆,动圆P与这两个定圆都相切,则圆P的圆心轨迹可能是( )


| A. | ①③⑤ | B. | ②④⑤ | C. | ①②④ | D. | ①②③ |
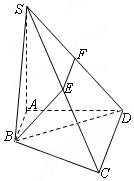 如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.
如图,四边形ABCD是梯形,AB∥CD,AB⊥AD,SA⊥平面ABCD,E、F分别是SC、SD的中点,SA=AD=2CD=4AB=4.