题目内容
9．若实数x、y满足$\left\{\begin{array}{l}{y≤x}\\{y≥\frac{1}{2}x}\\{x+y≤1}\end{array}\right.$，则z=2x-y的最大值为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
分析 作出可行域，变形目标函数，平移直线y=2x可得结论．
解答 
解：作出约束条件$\left\{\begin{array}{l}{y≤x}\\{y≥\frac{1}{2}x}\\{x+y≤1}\end{array}\right.$，所对应的可行域（如图△ABO），
变形目标函数可得y=2x-z，平移直线y=2x可知当直线经过点A时，
直线的截距最小，z取最大值，由$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{x+y=1}\end{array}\right.$可得$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{1}{3}}\end{array}\right.$，A（$\frac{2}{3}$，$\frac{1}{3}$）
代值计算可得z=2x-y的最大值为1，
故选：C．
点评 本题考查简单线性规划，准确作图是解决问题的关键，属中档题．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
20．函数y=xcosx-sinx的部分图象大致为（ ）
| A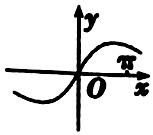． |  | B． |  | ||
| C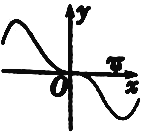． |  | D． |  |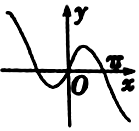
17．已知函数f（x）满足如下条件：①任意x∈R，有f（x）+f（-x）=0成立；②当x≥0时，f（x）=$\frac{1}{2}$（|x-m2|+|x-2m2|-3m2）；③任意x∈R，有f（x）≥f（x-1）成立．则实数m的取值范围（ ）
| A． | $[{-\frac{{\sqrt{6}}}{6}，\frac{{\sqrt{6}}}{6}}]$ | B． | $[{-\frac{1}{6}，\frac{1}{6}}]$ | C． | $[{-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}]$ | D． | $[{-\frac{1}{3}，\frac{1}{3}}]$ |
1．复数z=$\frac{1+i}{i}$，则|z|=（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | -$\sqrt{2}$ | D． | 1-i |