题目内容
15.据报道,某淡水湖的湖水在50年内减少了10%,若按此规律,设2013年的湖水量为m,从2013年起,经过x年后湖水量y与x的函数关系为( )| A. | y=0.9${\;}^{\frac{x}{50}}$ | B. | y=(1-0.1${\;}^{\frac{x}{50}}$)m | C. | y=0.9${\;}^{\frac{x}{50}}$m | D. | y=(1-0.150x)m |
分析 首先应该确定湖水量的年平均变化率,然后在建立湖水量y与x的函数关系即可.
解答 解:设淡水湖的湖水的年平均变化率为P,则P50=0.9,
∴P=${0.9}^{\frac{1}{50}}$,
∴设2013年的湖水量为m,经过x年后湖水量y与x的函数关系是y=m${•0.9}^{\frac{x}{50}}$
故选:C.
点评 本题考查的是根据实际问题选择函数模型的问题.在解答的过程当中充分体现了应用题的特点,平均变化率的求法以及指数型函数解析式是解答本题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
5.定义在R上的偶函数f(x)满足f(x+2)=f(x),且在[0,1]上单调递增,设a=f(3),b=f(1.2),c=f(2),则a,b,c大小关系是( )
| A. | b>c>a | B. | a>c>b | C. | a>b>c | D. | c>b>a |
10.函数f(x)的定义域为R,f(-1)=2015,对任意的x∈R.都有f′(x)<3x2成立,则不等式f(x)<x3+2016的解集为( )
| A. | (-1,+∞) | B. | (-1,0) | C. | (-∞,-1) | D. | (-∞,+∞) |
20.从班委会5名成员中选出3名,分别担任班级学习委员、文娱委员与体育委员,其中甲、乙二人不能担任文娱委员,则不同的选法共有( )种.
| A. | 20 | B. | 24. | C. | 36 | D. | 54 |
7.已知集合A={1,a2},实数a不能取的值的集合是( )
| A. | {-1,1} | B. | {-1} | C. | {-1,0,1} | D. | {1} |
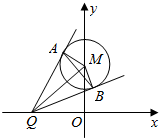 如图,已知圆M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别与圆M切于点AB.
如图,已知圆M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别与圆M切于点AB.