题目内容
8.定义在R上的奇函数y=f(x)满足f(4)=0,且当x>0时,不等式f(x)<xf′(x)恒成立,则函数g(x)=$\frac{f(x)}{x}$+e|x|-1的零点的个数为2.分析 根据题意,由奇函数的性质可得f(0)=0=f(4)=f(-4),令函数h(x)=$\frac{f(x)}{x}$,分析可得h(x)为偶函数,当x>0时,对其求导分析可得h′(x)>0,即可得x>0时,函数h(x)是增函数,结合偶函数的性质分析可得x<0时,h(x)是减函数,结合题意,即可得答案.
解答 解:根据题意,y=f(x)是R上的奇函数,
则有f(0)=0,且f(-x)=-f(x),
又由f(x)满足f(4)=0,
则有f(0)=0=f(4)=f(-4),
令函数h(x)=$\frac{f(x)}{x}$,h(-x)=$\frac{f(-x)}{-x}$=$\frac{f(x)}{x}$=h(x),
∴h(x)是偶函数,
又x>0时,f(x)<xf'(x)恒成立,
即xf'(x)-f(x)>0恒成立,
对于函数h(x),则有h′(x)>0,
则x>0时,函数h(x)是增函数,
故x<0时,h(x)是减函数,
函数g(x)=$\frac{f(x)}{x}$+e|x|-1的零点,
即h(x)与y=1-e|x|的交点,
画出函数的图象,如图所示:
结合函数图象得到h(x)与y=1-e|x|的交点有2个,
即函数g(x)=$\frac{f(x)}{x}$+e|x|-1的零点的个数为2个,
故答案为:2.
点评 本题考查函数零点个数的判定,涉及导数与函数单调性的性质,注意函数的单调性的充分应用.

练习册系列答案
相关题目
18.把5名人大代表派到3个城市作党的十八大宣讲报告,每个城市至少派一名,则不同的分派方法有( )
| A. | 150种 | B. | 90种 | C. | 60种 | D. | 180种 |
13.已知,在直角梯形ABCD中,BC∥AD,BC⊥CD,∠BAD=$\frac{π}{3}$,AB=2BC=2,动点P在以C为圆心且与直线BD相切的圆上运动,若$\overrightarrow{AP}$=α$\overrightarrow{AB}$+β$\overrightarrow{AD}$,则α+β的取值范围是( )
| A. | [0,1] | B. | [0,2] | C. | [1,2] | D. | (-∞,1]∪[2,+∞) |
18.下列集合A到B的对应中,不能构成映射的是( )


| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
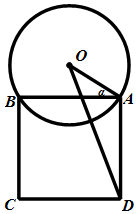 某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)
某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.) 在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点.
在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点.