题目内容
6.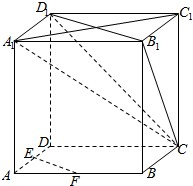 如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AB、AD的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AB、AD的中点.(1)求证:EF平行平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1
(3)求直线A1C与平面ABCD所成角的正切值.
分析 (1)推导出EF∥BD,BD∥B1D1,从而EF∥B1D1,由此能证明EF∥平面CB1D1.
(2)推导出B1D1⊥A1C1,AA1⊥B1D1,由此能证明平面CAA1C1⊥平面CB1D1.
(3)由AA1⊥底面ABCD,得∠A1CA是直线A1C与平面ABCD所成角,由此能求出直线A1C与平面ABCD所成角的正切值.
解答 证明:(1)在正方体ABCD-A1B1C1D1中,
∵E、F分别为棱AB、AD的中点,∴EF∥BD,
∵BD∥B1D1,∴EF∥B1D1,
∵EF?平面CB1D1,B1D1?平面CB1D1,
∴EF∥平面CB1D1.
(2)∵正方体ABCD-A1B1C1D1中,四边形A1B1C1D1是正方形,
∴B1D1⊥A1C1,AA1⊥B1D1,
∵AA1∩A1C1=A1,B1D1⊥平面CAA1C1,
∴B1D1?平面A1B1C1D1,
∴平面CAA1C1⊥平面CB1D1.
解:(3)∵AA1⊥底面ABCD,
∴∠A1CA是直线A1C与平面ABCD所成角,
设正方体ABCD-A1B1C1D1中棱长为a,
则AA1=a,AC=$\sqrt{{a}^{2}+{a}^{2}}$=$\sqrt{2}a$,
tan∠A1CA=$\frac{A{A}_{1}}{AC}$=$\frac{a}{\sqrt{2}a}$=$\frac{\sqrt{2}}{2}$.
∴直线A1C与平面ABCD所成角的正切值为$\frac{\sqrt{2}}{2}$.
点评 本题考查线面平行、面面垂直的证明,考查线面角的正切值的求法,是中档题,解题时要认真审题,注意空是思维能力的培养产.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
17.已知函数f(x)在其定义域(-∞,0)上是减函数,且f(1-m)<f(m-3),则实数m的取值范围是( )
| A. | (-∞,2) | B. | (0,1) | C. | (0,2) | D. | (1,2) |
1.与函数y=$\frac{1}{\sqrt{x-1}}$的定义域相同的函数是( )
| A. | y=$\sqrt{x-1}$ | B. | y=2x-1 | C. | y=$\frac{1}{x-1}$ | D. | y=ln(x-1) |
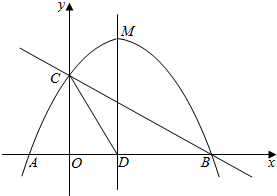 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于点A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于点A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2).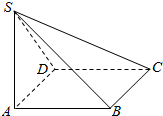 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是正方形,且SA=AB=2.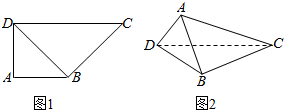 如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.
如图,在直角梯形ABCD中,AB⊥AD,AB=AD=2,CD=4,将三角形ABD沿BD翻折,使面ABD⊥面BCD.