题目内容
如图,在四棱锥 中,
中, ,四边形
,四边形 是菱形,
是菱形, ,且
,且 交于点
交于点 ,
, 是
是 上任意一点.
上任意一点.
(1)求证: ;
;
 (2)已知二面角
(2)已知二面角 的余弦值为
的余弦值为 ,若
,若 为
为 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
解:(1)因为 平面
平面 ,所以
,所以 ,因为四边形
,因为四边形 为菱形,所以
为菱形,所以 又
又 因为
因为 5分
5分
(2)连接 在
在 中,
中, 所以
所以 分别以
分别以 所在直线为
所在直线为 轴,
轴, 轴,
轴, 轴建立如图所示的空间直角坐标系,设
轴建立如图所示的空间直角坐标系,设 则
则 ,
, ,由(1)知,平面
,由(1)知,平面 的一个法向量为
的一个法向量为 得
得 ,令
,令 ,得
,得 ……8分
……8分
因为二面角 的余弦值为
的余弦值为 ,所以
,所以 ,
,
解得 或
或 (舍去),所以
(舍去),所以 …………10分
…………10分
设 与平面
与平面 所成的角为
所成的角为 .因为
.因为 ,
, ,所以
,所以 所以
所以 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .12分
.12分

练习册系列答案
相关题目
 左支上一点P到其左、右两焦点F1、F2的距离之和为8,
左支上一点P到其左、右两焦点F1、F2的距离之和为8, B.
B.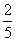 C.
C. D.
D.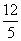
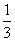 B.
B.  C.
C. 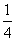 D.
D. 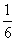
 3门课由于上课时间相同,至多选1门,若学校规定每位学生选修4门,不同选修方案共有 种.
3门课由于上课时间相同,至多选1门,若学校规定每位学生选修4门,不同选修方案共有 种. ,
, ,则
,则
 B.
B. C.
C. D.
D.
 的图象可能是
的图象可能是
 中,角
中,角 所对的边为
所对的边为 .若
.若 ,则
,则
 B.
B. C.
C. D.
D. ( )
( )  的对应点位于( )
的对应点位于( )