题目内容
17.若偶函数y=f(x),x∈R,满足f(x+2)=-f(x),且x∈[0,2]时,f(x)=3-x2,函数g(x)=sin(|x|),则使方程f(x)=g(x)在[-10,10]内根的个数为( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 根据条件求出函数的周期性,根据函数的奇偶性和周期性的关系求出函数在一个周期内的解析式,利用数形结合斤求解即可.
解答 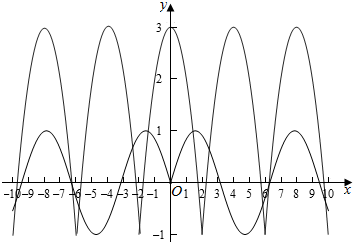 解:由f(x+2)=-f(x),得f(x+4)=-f(x+2)=-[-f(x)]=f(x),
解:由f(x+2)=-f(x),得f(x+4)=-f(x+2)=-[-f(x)]=f(x),
即函数f(x)的周期是4.
若x∈[-2,0],则-x∈[0,2],
即f(-x)=3-x2,
∵f(x)是偶函数,
∴f(-x)=3-x2=f(x),
即f(x)=3-x2,x∈[-2,0],
∴f(x)=3-x2,x∈[-2,2],
作出函数f(x)和g(x)=sin(|x|)在[-10,10]上的图象如图:
则两个函数的交点个数为10个,
故方程f(x)=g(x)在[-10,10]内根的个数为10个,
故选:D.
点评 本题主要考查函数解析式的求解,函数奇偶性的性质,以及函数与方程的应用,利用数形结合是解决本题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
8.已知向量$\overrightarrow{a}$=(-1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
5.“x<1”是“|x|<2”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
12.设α,β是两个不同的平面,直线m⊥α,则“m⊥β”是“α∥β”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
6.在平面直角坐标系xOy中,已知圆C:(x-3)2+y2=4,点A,B在圆C上,且$|{AB}|=2\sqrt{3}$,则$|{\overrightarrow{OA}+\overrightarrow{OB}}|$的最大值是( )
| A. | 8 | B. | $4\sqrt{2}$ | C. | 4 | D. | $2\sqrt{2}$ |