题目内容
9.若$\frac{1}{a}<\frac{1}{b}<0$,则下列不等式:①a+b<ab;②|a|<|b|;③a<b;④$\frac{b}{a}+\frac{a}{b}>2$中,正确不等式的序号是( )| A. | ①② | B. | ②③ | C. | ③④ | D. | ①②④ |
分析 若$\frac{1}{a}<\frac{1}{b}<0$,则a<0,b<0,且a>b则①a+b为负数,ab为正数;②绝对值的意义判断,③赋值来处理;④借助于均值不等式来处理.
解答 解:若$\frac{1}{a}<\frac{1}{b}<0$,则a<0,b<0,且a>b
则①a+b<0,ab>0,故①正确;
②a<0,b<0,且a>b,显然|a|<|b|,故②正确;
③由②得a>b,故③错;
④由于a<0,b<0,故$\frac{b}{a}$>0,$\frac{a}{b}$>0
则$\frac{b}{a}$+$\frac{a}{b}$≥2$\sqrt{\frac{b}{a}•\frac{a}{b}}$=2(当且仅当$\frac{b}{a}$=$\frac{a}{b}$即a=b时取“=”)
又a>b,则$\frac{b}{a}$+$\frac{a}{b}$>2,故④正确;
故选:D.
点评 本题考查不等式的性质,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
16.已知函数a,b,则“|a+b|+|a-b|≤1”是“a2+b2≤1“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.设a≠0,a∈R,则抛物线y=ax2的焦点坐标为( )
| A. | (0,$\frac{1}{4a}$) | B. | ($\frac{a}{2}$,0) | C. | (0,$\frac{1}{2a}$) | D. | ($\frac{a}{4}$,0) |
1.已知随机变量X的分布列如下:
则a=$\frac{25}{84}$,数学期望E(X)=$\frac{65}{42}$.
| X | 1 | 2 | 3 | 4 |
| P | $\frac{49}{84}$ | a | $\frac{9}{84}$ | $\frac{1}{84}$ |
18.下列说法错误的是( )
| A. | 命题“?x∈R,x2-2x+1<0”的否定是“?x∈R,x2-2x+1≥0” | |
| B. | 命题“若m>0,则方程x2+x-m=0有实根”的逆命题为真命题 | |
| C. | 命题“若a>b,则ac2>bc2”的否命题为真命题 | |
| D. | 若命题“¬p∨q”为假命题,则“p∧¬q”为真命题 |
19.若$\frac{1}{a}$<$\frac{1}{b}$<0,则下列结论正确的是( )
| A. | |a|>|b| | B. | $\frac{b}{a}$<1 | C. | ab<b2 | D. | ab>b2 |
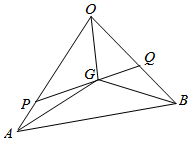 已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,点G是△OAB的重心,过点G的直线PQ与OA、OB分别交于P、Q两点.
已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,点G是△OAB的重心,过点G的直线PQ与OA、OB分别交于P、Q两点.