题目内容
在正三棱锥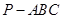 中,有一半球,其底面与正三棱锥的底面重合,正三棱锥的三个侧面都和半球相切。如果半球的半径等于1,则当正三棱锥的体积最小时,正三棱锥的高等于( )
中,有一半球,其底面与正三棱锥的底面重合,正三棱锥的三个侧面都和半球相切。如果半球的半径等于1,则当正三棱锥的体积最小时,正三棱锥的高等于( )
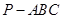 中,有一半球,其底面与正三棱锥的底面重合,正三棱锥的三个侧面都和半球相切。如果半球的半径等于1,则当正三棱锥的体积最小时,正三棱锥的高等于( )
中,有一半球,其底面与正三棱锥的底面重合,正三棱锥的三个侧面都和半球相切。如果半球的半径等于1,则当正三棱锥的体积最小时,正三棱锥的高等于( )A.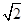 | B.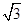 | C.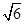 | D.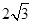 |
B
 |
设球心为


 中点为
中点为 连接
连接 则
则 是锥高,设为
是锥高,设为
 设
设


 又
又 ,
, ,则
,则 所以正三棱锥的体积为
所以正三棱锥的体积为 ;
; ;
; 时,
时, 函数
函数 是减函数;
是减函数; 时,
时, 函数
函数 是减函数;所以当
是减函数;所以当 时,
时, 取最小值.故当正三棱锥的体积最小时,正三棱锥的高等于
取最小值.故当正三棱锥的体积最小时,正三棱锥的高等于 故选B
故选B
练习册系列答案
相关题目
 各边
各边 上分别取
上分别取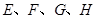 四点,如果与
四点,如果与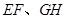 能相交于点
能相交于点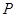 ,那么
,那么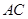 上
上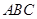 内
内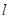 、
、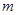 与平面
与平面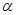 和
和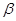 的命题中,真命题的是( )
的命题中,真命题的是( )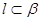 且
且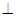
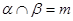 且
且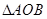 中,
中,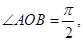 AB=2OB=4,D为AB的中点,若
AB=2OB=4,D为AB的中点,若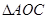 是
是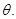 (I)若
(I)若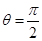 ,求证:平面
,求证:平面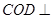 平面AOB;(II)若
平面AOB;(II)若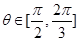 时,求二面角C—OD—B的余弦值的最小值。
时,求二面角C—OD—B的余弦值的最小值。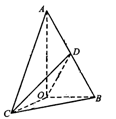
 中,底面
中,底面 是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.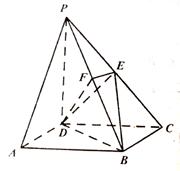
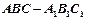 的三视图如图所示,
的三视图如图所示, 其中正视图
其中正视图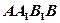 和侧视图
和侧视图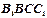 均为矩形,俯视图
均为矩形,俯视图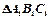 中,
中,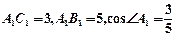 。
。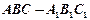 中,求证:
中,求证: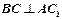 ;
;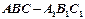 中,若
中,若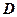 是底边
是底边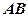 的中点,求证:
的中点,求证: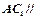 平面
平面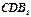 ;
;
 的底面面积为16,一条侧棱长为
的底面面积为16,一条侧棱长为 ,则它的斜高为
,则它的斜高为 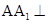 面ABC,高为5,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为_______
面ABC,高为5,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为_______