题目内容
已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:由E为AB的中点,可取AD中点F,连接EF,则∠CEF为异面直线CE与BD所成角,设出正四面体的棱长,求出△CEF的三边长,然后利用余弦定理求解异面直线CE与BD所成角的余弦值.
解答:
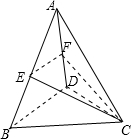 解:如图,
解:如图,
取AD中点F,连接EF,CF,
∵E为AB的中点,
∴EF∥DB,
则∠CEF为异面直线BD与CE所成的角,
∵ABCD为正四面体,E,F分别为AB,AD的中点,
∴CE=CF.
设正四面体的棱长为2a,
则EF=a,
CE=CF=
=
a.
在△CEF中,由余弦定理得:
cos∠CEF=
=
=
.
故选:B.
 解:如图,
解:如图,取AD中点F,连接EF,CF,
∵E为AB的中点,
∴EF∥DB,
则∠CEF为异面直线BD与CE所成的角,
∵ABCD为正四面体,E,F分别为AB,AD的中点,
∴CE=CF.
设正四面体的棱长为2a,
则EF=a,
CE=CF=
| (2a)2-a2 |
| 3 |
在△CEF中,由余弦定理得:
cos∠CEF=
| CE2+EF2-CF2 |
| 2CE•EF |
| a2 | ||
2×
|
| ||
| 6 |
故选:B.
点评:本题考查异面直线及其所成的角,关键是找角,考查了余弦定理的应用,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
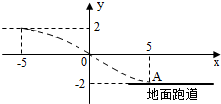 如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )
如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=-
|
复数(3+2i)i等于( )
| A、-2-3i | B、-2+3i |
| C、2-3i | D、2+3i |
复数z=(3-2i)i的共轭复数
等于( )
. |
| z |
| A、-2-3i | B、-2+3i |
| C、2-3i | D、2+3i |
设z=
,则z的共轭复数为( )
| 10i |
| 3+i |
| A、-1+3i | B、-1-3i |
| C、1+3i | D、1-3i |
