题目内容
 底面边长为2的正三棱锥P-ABC,其表面展开图是三角形P1P2P3,如图,求△P1P2P3的各边长及此三棱锥的体积V.
底面边长为2的正三棱锥P-ABC,其表面展开图是三角形P1P2P3,如图,求△P1P2P3的各边长及此三棱锥的体积V.考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:利用侧面展开图三点共线,判断△P1P2P3是等边三角形,然后求出边长,利用正四面体的体积求出几何体的体积.
解答:
解:根据题意可得:P1,B,P2共线,∵∠ABP1=∠BAP1=∠CBP2,∠ABC=60°,
∴∠ABP1=∠BAP1=∠CBP2=60°,
∴∠P1=60°,同理∠P2=∠P3=60°,
∴△P1P2P3是等边三角形,P-ABC是正四面体,
∴△P1P2P3的边长为4,
VP-ABC=
×AB3=
∴∠ABP1=∠BAP1=∠CBP2=60°,
∴∠P1=60°,同理∠P2=∠P3=60°,
∴△P1P2P3是等边三角形,P-ABC是正四面体,
∴△P1P2P3的边长为4,
VP-ABC=
| ||
| 12 |
2
| ||
| 3 |
点评:本题考查空间想象能力以及逻辑推理能力,几何体的侧面展开图和体积的求法.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知集合A={y丨y=x2},B={x丨
<0},求A∩B=( )
| x+1 |
| x-2 |
| A、[0,+∞) |
| B、(-1,2) |
| C、[0,2) |
| D、(-1,0] |
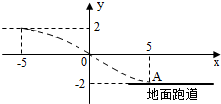 如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )
如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=-
|