题目内容
5.对任意实数a,b,c,d,命题:①若a>b,c≠0,则ac>bc;
②若a>b,则ac2>bc2;
③若ac2>bc2,则a>b.
其中真命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 利用不等式的基本性质,结合反例判断求解即可.
解答 解:①若a>b,c≠0,当c<0时,ac>bc不成立;
②若a>b,则ac2>bc2;当c=0时,不等式不成立;
③若ac2>bc2,可知c≠0,c2>0,则a>b.正确;
故选:B.
点评 本题考查表达式的基本性质的应用,是基础题.

练习册系列答案
相关题目
20.已知函数f(x)=x3-3ax+$\frac{1}{4}$,若x轴为曲线y=f(x)的切线,则a的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{3}{4}$ | D. | $\frac{1}{4}$ |
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为E,F,以OF(O为坐标原点)为直径的圆C角双曲线于A,B两点,AE与圆C相切,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{2}+3\sqrt{6}}{2}$ | B. | $\frac{2\sqrt{2}+\sqrt{6}}{2}$ | C. | $\frac{3\sqrt{2}+\sqrt{6}}{2}$ | D. | $\frac{3\sqrt{2}+2\sqrt{6}}{2}$ |
17.如图中的程序框图表示求三个实数a,b,c中最大数的算法,那么在空白的判断框中,应该填入( )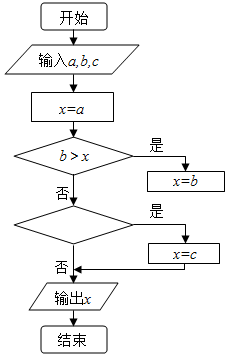

| A. | a>x | B. | b>x | C. | c<x | D. | c>x |
14.执行如图所示程序框图,则输出的结果是( )


| A. | $\frac{1}{6}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{10}$ | D. | $\frac{11}{12}$ |