Question

如图，正方形ABCD的边长为1，延长BA至E，使AE=1，连接EC、ED，则sin∠CED=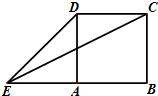

 

．

Answer 1

考点：两角和与差的正弦函数

专题：三角函数的求值

分析：根据两角和差的正弦公式进行求解即可．

解答： 解：由条件知AC=

5

，sin∠CEB=

1

5

=

5

5

，cos∠CEB=

2 5

5

，
∵∠DEA=

π

4

，
∴∠CED=

π

4

-∠CEB，
则sin∠CED=sin（

π

4

-∠CEB）=

2

2

（cos∠CEB-sin∠CEB）=

2

2

（

2 5

5

-

5

5

）=

2

2

×

5

5

=

10

10

，
故答案为：

10

10

点评：本题主要考查三角函数的求值，利用两角和差的正弦公式是解决本题的关键．