Question

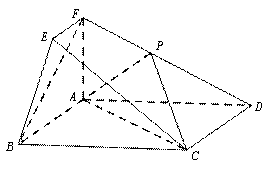
在如图所示的几何体中，四边形ABCD为矩形，平面ABEF⊥平面ABCD， EF // AB，∠BAF=90º， AD= 2，AB=AF=2EF =1，点P在棱DF上．

（1）若P是DF的中点， 求异面直线BE与CP所成角的余弦值；

（2）若二面角D-AP-C的余弦值为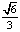，求PF的长度．

 

Answer 1

解析：（1）因为∠BAF=90º，所以AF⊥AB，    

因为 平面ABEF⊥平面ABCD，且平面ABEF ∩平面ABCD= AB， 

所以AF⊥平面ABCD，因为四边形ABCD为矩形，

所以以A为坐标原点，AB，AD，AF分别

为x，y，z轴，建立如图所示空间直角坐标系．

所以 ，，，．

所以 ，，

所以，

即异面直线BE与CP所成角的余弦值为． ----6分                                             

（2）因为AB⊥平面ADF，所以平面APF的法向量为．

设P点坐标为，在平面APC中，，，

所以 平面APC的法向量为，  

所以，

解得，或（舍）．   所以．       -------------------------12分