已知x.y都是正数.且lnx+lny=ln(x+y).则4x+y的最小值为( )A．6B．8C．9D．10 题目和参考答案——青夏教育精英家教网—

题目内容

1．已知x，y都是正数，且lnx+lny=ln（x+y），则4x+y的最小值为（　　）

A．

B．

C．

D．

分析利用对数的运算法则得到m，n的关系式，利用基本不等式求解最小值即可．

解答解：x，y都是正数，且lnx+lny=ln（x+y），
可得xy=x+y，即$\frac{1}{x}+\frac{1}{y}$=1
则4x+y=（4x+y）（$\frac{1}{x}+\frac{1}{y}$）=5+$\frac{4x}{y}+\frac{y}{x}$≥5+2$\sqrt{\frac{4x}{y}•\frac{y}{x}}$=9．
当且仅当x=$\frac{3}{2}$，y=3是取等号．
故选：C．

点评本题考查基本不等式在最值中的应用，考查转化思想以及计算能力．

练习册系列答案

6．已知函数f（x）=xlnx-k（x-1）
（1）求f（x）的单调区间；并证明lnx+$\frac{e}{x}$≥2（e为自然对数的底数）恒成立；
（2）若函数f（x）的一个零点为x₁（x₁＞1），f'（x）的一个零点为x₀，是否存在实数k，使$\frac{x_1}{x_0}$=k，若存在，求出所有满足条件的k的值；若不存在，说明理由．

9．已知平面直角坐标系中两定点为A（2，3），B（5，3），若动点M满足|AM|=2|BM|．
（1）求动点M的轨迹方程；
（2）若直线l：y=x-5与M的轨迹交于C，D两点，求CD的长度．

16．已知以下列联表，且已知P（K²≥6.635）≈0.010，根据此列联表求得随机变量K²的观测值k≈16.373＞6.635，那么以下说法正确的是（　　）

	患心脏病	患其它病	总计
秃顶	214	175	389
不秃顶	451	597	1048
总计	665	772	1437

	A．	秃顶与患心脏病一定有关系
	B．	在犯错误的概率不超过0.010的前提下，认为秃顶与患心脏病有关系
	C．	我们有1%的把握认为秃顶与患心脏病有关系
	D．	在犯错误的概率不超过0.010的前提下，认为秃顶与患心脏病没有关系

6．已知F₁、F₂为双曲线C：x²-y²=2的左、右焦点，点P在C上，|PF₁|=2|PF₂|，则△F₁PF₂的形状为（　　）

13．

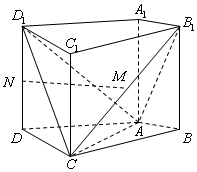如图，在四棱柱ABCD-A₁B₁C₁D₁中，侧棱A₁A⊥底面ABCD，AB⊥AC，AB=3，AC=AA₁=6，AD=CD=5，且点M和N分别为B₁C和D₁D的中点．
（1）求证：MN∥平面ABCD；
（2）求二面角D₁-AC-B₁的正切值．

10．计算下列各式：
（1）（2a${\;}^{\frac{2}{3}}$b${\;}^{\frac{1}{2}}$）（-6a${\;}^{\frac{1}{2}}$b${\;}^{\frac{1}{3}}$）÷（-3a${\;}^{\frac{1}{6}}$b${\;}^{\frac{5}{6}}$）（a＞0，b＞0）
（2）$2{（{lg\sqrt{2}}）^2}+lg\sqrt{2}×lg5+\sqrt{{{（{lg\sqrt{2}}）}^2}-lg2+1}$．

11．

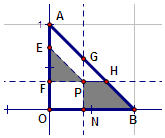△AOB是直角边长为1的等腰直角三角形，在坐标系中位置如图所示，O为坐标原点，P（a，b）是三角形内任意一点，且满足b=2a，过P点分别做OB，OA，AB三边的平行线，求阴影部分面积的最大值及此时P点坐标．

试题分类