题目内容
10.在数列{an}中,已知a1=1,前n项和Sn满足${S}_{n}^{2}$=an(Sn-$\frac{1}{2}$)(n≥2),则Sn=$\frac{1}{3-2n}$.分析 由${S}_{n}^{2}$=an(Sn-$\frac{1}{2}$)(n≥2),可得 ${S}_{n}^{2}$=(Sn-Sn-1)(Sn-$\frac{1}{2}$)(n≥2),变形为:$\frac{1}{{S}_{n}}-\frac{1}{{S}_{n-1}}$=-2,再利用等差数列的通项公式即可得出.
解答 解:∵${S}_{n}^{2}$=an(Sn-$\frac{1}{2}$)(n≥2),
∴${S}_{n}^{2}$=(Sn-Sn-1)(Sn-$\frac{1}{2}$)(n≥2),
化为:2SnSn-1-Sn+Sn-1=0,
∴$\frac{1}{{S}_{n}}-\frac{1}{{S}_{n-1}}$=-2,
∴数列$\{\frac{1}{{S}_{n}}\}$是等差数列,首项为1,公差为-2.
∴$\frac{1}{{S}_{n}}$=1-2(n-1)=3-2n.
∴Sn=$\frac{1}{3-2n}$.
故答案为:$\frac{1}{3-2n}$.
点评 本题考查了等差数列的通项公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.已知点(a,1)到直线x-y+1=0的距离为1,则a的值为( )
| A. | 1 | B. | -1 | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |
18.圆(x-2)2+y2=5与直线y=2x+1的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 直线过圆心 |
5.若函数f(x)=x(lnx-ax)在区间(0,e)上有两个不同的极值点,则实数a的取值范围是( ) (e是自然对数的底数)
| A. | $(\frac{1}{2e},\frac{1}{2})$ | B. | $(0,\frac{1}{2})$ | C. | $(\frac{1}{2e},+∞)$ | D. | $(\frac{1}{e},\frac{1}{2})$ |
15.已知复数z满足z-i=iz+3,则$\overline{z}$=( )
| A. | 1+2i | B. | 1-2i | C. | 2+2i | D. | 2-2i |
19.若函数f(x)=2x+b-1(b∈R)的图象不经过第二象限,则有( )
| A. | b≥1 | B. | b≤1 | C. | b≥0 | D. | b≤0 |
20.函数y=2lnx-$\frac{1}{{x}^{2}}$的零点所在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
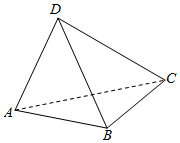 如图,在三棱锥D-ABC中,已知AB=2,$\overrightarrow{AC}$•$\overrightarrow{BD}$=-3,设AD=a,BC=b,CD=c,则$\frac{c^2}{ab+1}$的最小值为2.
如图,在三棱锥D-ABC中,已知AB=2,$\overrightarrow{AC}$•$\overrightarrow{BD}$=-3,设AD=a,BC=b,CD=c,则$\frac{c^2}{ab+1}$的最小值为2.