题目内容
如图所示．在△ABC中∠C=90°，∠A的平分线AE交BA上的高CH于D点，过D引AB的平行线交BC于F．求证：BF=EC．考点：相似三角形的性质,相似三角形的判定
专题：立体几何
分析：如图所示，由AE是∠A的平分线，可得
=
，
=
．在△ABC中∠C=90°，CH⊥AB．利用射影定理可得：
=
．于是
=
．由DF∥AB，可得
=
，因此
=
，展开即可证明．
| BE |
| EC |
| AB |
| AC |
| AC |
| AH |
| CD |
| DH |
| AB |
| AC |
| AC |
| AH |
| BE |
| EC |
| CD |
| DH |
| CD |
| DH |
| CF |
| BF |
| BE |
| EC |
| CF |
| BF |
解答：
证明：如图所示，
由AE是∠A的平分线，
∴
=
，
=
，
∵在△ABC中∠C=90°，CH⊥AB．
∴AC2=AH•AB，即
=
．
∴
=
．
∵DF∥AB，
∴
=
，
∴
=
，
∴（BF+FE）•BF=EC•（EC+EF），
∴（BF-EC）•BC=0，
∴BF=EC．
由AE是∠A的平分线，
∴
| BE |
| EC |
| AB |
| AC |
| AC |
| AH |
| CD |
| DH |
∵在△ABC中∠C=90°，CH⊥AB．
∴AC2=AH•AB，即
| AB |
| AC |
| AC |
| AH |
∴
| BE |
| EC |
| CD |
| DH |
∵DF∥AB，
∴
| CD |
| DH |
| CF |
| BF |
∴
| BE |
| EC |
| CF |
| BF |
∴（BF+FE）•BF=EC•（EC+EF），
∴（BF-EC）•BC=0，
∴BF=EC．
点评：本题考查了角平分线的性质、射影定理、平行线分线段成比例定理，考查了推理能力和计算能力，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
抛物线E：y2=4x的焦点为F，准线l与x轴的交点为A．点C在抛物线E上，以为圆心，|CO|为半径作圆．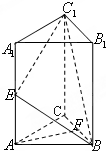
如图，在正三棱柱ABC-A1B1C1中，AB=2，AA1=4，E、F分别为AA1、BC的中点．