题目内容
 已知正△PAB与△ABC所在平面垂直,且AB=
已知正△PAB与△ABC所在平面垂直,且AB=| 3 |
(Ⅰ)求证:BC⊥PA;
(Ⅱ)求异面直线MN与PA所成的角.
考点:直线与平面垂直的性质,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(Ⅰ)证明BC⊥AB,利用仔细与平面垂直的性质定理证明BC⊥平面PAB,推出BC⊥PA.
(Ⅱ)取AB中点O,连接MO,NO,得到∠MNO为异面直线MN与PA所成的角,通过解三角形求解即可.
(Ⅱ)取AB中点O,连接MO,NO,得到∠MNO为异面直线MN与PA所成的角,通过解三角形求解即可.
解答:
 解:(Ⅰ)∵AB=
解:(Ⅰ)∵AB=
,AC=2,BC=1,∴AB2+BC2=AC2,
∴BC⊥AB …(3分)
又∵面PAB⊥面ABC,交线为AB,BC?面ABC
∴BC⊥平面PAB.…(6分)
∴BC⊥PA.…(7分)
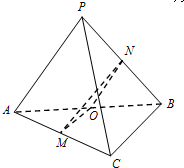
(Ⅱ)取AB中点O,连接MO,NO,
∵N是PB的中点,∴NO∥PA,
∴∠MNO为异面直线MN与PA所成的角.…(10分)
∵MO∥BC,由(Ⅰ)可得MO⊥平面PAB.
在直角三角形MNO中,MO=
,NO=
,
∴tan∠MNO=
,∠MNO=30°,
∴异面直线MN与PA所成的角为30°.…(14分)
 解:(Ⅰ)∵AB=
解:(Ⅰ)∵AB=| 3 |
∴BC⊥AB …(3分)
又∵面PAB⊥面ABC,交线为AB,BC?面ABC
∴BC⊥平面PAB.…(6分)
∴BC⊥PA.…(7分)
(Ⅱ)取AB中点O,连接MO,NO,
∵N是PB的中点,∴NO∥PA,
∴∠MNO为异面直线MN与PA所成的角.…(10分)
∵MO∥BC,由(Ⅰ)可得MO⊥平面PAB.
在直角三角形MNO中,MO=
| 1 |
| 2 |
| ||
| 2 |
∴tan∠MNO=
| ||
| 3 |
∴异面直线MN与PA所成的角为30°.…(14分)
点评:本题考查直线与平面垂直的判定与性质的应用,异面直线所成角的求法,考查计算能力.

练习册系列答案
相关题目
下列函数在区间(0,+∞)上为增函数的是( )
| A、y=1-2x | ||
| B、y=x2+2x | ||
| C、y=-x2 | ||
D、y=
|
读如图程序,当输入的x为60时,输出y的值为( )


| A、30 | B、31 | C、36 | D、61 |