题目内容
6.下列直线中与直线l:3x+2y-5=0相交的是③(填上正确的序号).①y=-$\frac{3}{2}$x+5②3x+2y=0 ③$\frac{x}{3}$+$\frac{y}{2}$=1④$\frac{x}{2}$+$\frac{y}{3}$=1.
分析 直线l的斜率k=-$\frac{3}{2}$,要使直线与l相交,则所求直线的斜率k′≠-$\frac{3}{2}$.求出直线的斜率,即可得出结论.
解答 解:直线l的斜率k=-$\frac{3}{2}$,要使直线与l相交,则所求直线的斜率k′≠-$\frac{3}{2}$.
又①、②、④中直线的斜率都等于-$\frac{3}{2}$,③中直线的斜率等于-$\frac{2}{3}$,
故答案为③.
点评 本题考查直线的斜率,考查直线的位置关系,比较基础.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{4}=1$的一条渐近线为$y=\frac{1}{2}x$,则双曲线方程为( )
| A. | $\frac{x^2}{4}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | C. | $\frac{y^2}{16}-\frac{x^2}{4}=1$ | D. | $\frac{y^2}{4}-\frac{x^2}{16}=1$ |
17.若$\sqrt{3}$是3a与3b的等比中项,则a+b的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | $\frac{1}{2}$ |
1.已知△ABC的内角A,B,C满足10sinA=12sinB=15sinC,则cosB=( )
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\frac{9}{16}$ | C. | $\frac{{3\sqrt{15}}}{16}$ | D. | $\frac{5}{48}$ |
16.下列四个命题中错误的是( )
| A. | 在一次试卷分析中,从每个考室中抽取第5号考生的成绩进行统计,不是简单随机抽样 | |||||||||||||||||||
| B. | 对一个样本容量为100的数据分组,各组的频数如下:
| |||||||||||||||||||
| C. | 设产品产量与产品质量之间的线性相关系数为-0.91,这说明二者存在着高度相关 | |||||||||||||||||||
| D. | 通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如表列联表:
|
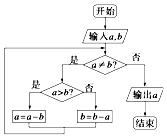 右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于2.
右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于2.