题目内容
11.在0,1,2,3,…,9这十个自然数中,任取三个不同的数字.则组成的三位数中是3的倍数的有228个.分析 要想组成的三位数能被3整除,把0,1,2,3,…,9这十个自然数中分为三组:0,3,6,9;1,4,7;2,5,8.求出每组中各取一个数,含0,与每组中各取一个数不含0以及从每组中各取三个数的所求可能,相加即可
解答 解:要想组成的三位数能被3整除,把0,1,2,3,…,9
这十个自然数中分为三组:0,3,6,9;1,4,7;2,5,8.
若每组中各取一个数,含0,共有C31C31C21A22=36种;
若每组中各取一个数不含0,共有C31C31C31A33=162种;
若从每组中各取三个数,共有3A33+C32A22A22=30种.
所以组成的三位数能被3整除,共有36+162+30=228种.
故答案为:228.
点评 本题考查了分步和分类计数原理,考查了计算能力,属于中档题

练习册系列答案
相关题目
1.已知两个单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为60°,且满足$\overrightarrow{{e}_{1}}$⊥(λ$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$),则实数λ的值是( )
| A. | -2 | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
2.函数y=lnx-x在x∈(0,e]上的最大值为( )
| A. | e | B. | 1 | C. | -e | D. | -1 |
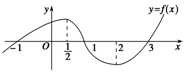
3. 已知函数f(x)在R上恒小于0,且f'(x)的图象如图,则|f(x)|的极大值点的个数为( )
已知函数f(x)在R上恒小于0,且f'(x)的图象如图,则|f(x)|的极大值点的个数为( )
 已知函数f(x)在R上恒小于0,且f'(x)的图象如图,则|f(x)|的极大值点的个数为( )
已知函数f(x)在R上恒小于0,且f'(x)的图象如图,则|f(x)|的极大值点的个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
1.已知函数$f(x)={e^x}-\frac{1}{2}{x^2}-mx$有极值点,则实数m的取值范围是( )
| A. | m≥1 | B. | m>1 | C. | 0≤m≤1 | D. | 0<m<1 |