题目内容
20.执行如图所示的程序框图,如果随机输入的t∈[-2,2],则事件“输出的S∈(-1,7]”发生的概率为( )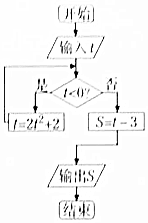
| A. | $\frac{1}{2}$ | B. | $\frac{4}{5}$ | C. | $\frac{8}{9}$ | D. | $\frac{2}{3}$ |
分析 根据程序框图,分析程序的功能,结合输出自变量的范围条件,利用函数的性质即可得到输出S∈[-3,-1]∪(2,10],区间长为10,即可求出概率.
解答 解:若0≤t≤2,则不满足条件输出S=t-3∈[-3,-1],
若-2≤t<0,则满足条件,此时t=2t2+2∈(2,10],此时不满足条件,
∴输出S∈[-3,-1]∪(2,10],区间长为10,
∴事件“输出的S∈(-1,7]”发生的概率为$\frac{7+1}{10}$=$\frac{4}{5}$.
故选B.
点评 本题主要考查概率的计算,考查程序框图的识别和判断,利用函数的取值范围是解决本题的关键,属于基础题.

练习册系列答案
相关题目
11.设非等腰△ABC的内角A、B、C所对边的长分别为a、b、c,且A、B、C成等差数列,用分析法证明:$\frac{1}{a-b}+\frac{1}{c-b}$=$\frac{3}{a-b+c}$.
15.小明有中国古代四大名著:《三国演义》,《西游记》,《水浒传》,《红楼梦》各一本,他要将这四本书全部借给三位同学,每位同学至少一本,但《西游记》,《红楼梦》这两本书不能借给同一人,则不同的借法有( )
| A. | 36种 | B. | 30种 | C. | 24种 | D. | 12种 |
5.某个零件的三视图如图所示,网格上小正方形的边长为1,则该零件的体积等于( )


| A. | 24-2π | B. | 24-4π | C. | 32-2π | D. | 48-4π |
9.已知x,y∈R,x2+y2+xy=315,则x2+y2-xy的最小值是( )
| A. | 35 | B. | 105 | C. | 140 | D. | 210 |
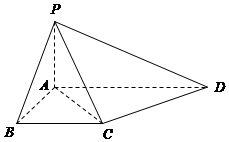 AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若 PA=AB=BC=$\frac{1}{2}$AD.
AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若 PA=AB=BC=$\frac{1}{2}$AD.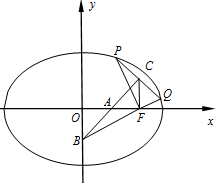 已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F的坐标为(1,0),P,Q为椭圆上位于y轴右侧的两个动点,使PF⊥QF,C为PQ中点,线段PQ的垂直平分线交x轴,y轴于点A,B(线段PQ不垂直x轴),当Q运动到椭圆的右顶点时,$|PF|=\frac{{\sqrt{2}}}{2}$.
已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F的坐标为(1,0),P,Q为椭圆上位于y轴右侧的两个动点,使PF⊥QF,C为PQ中点,线段PQ的垂直平分线交x轴,y轴于点A,B(线段PQ不垂直x轴),当Q运动到椭圆的右顶点时,$|PF|=\frac{{\sqrt{2}}}{2}$.