题目内容
已知p：a＝0，q：直线l1：x－2ay－1＝0与直线l2：2x－2ay－1＝0平行，求证：p
是q的充要条件．
证明 (1)当a＝0时，l1：x＝1，l2：x＝
，
所以l1∥l2，即由“a＝0”能推出“l1∥l2”．
(2)当l1∥l2时，若a≠0，
则l1∶y＝
x－，l2：y＝
x－，
所以＝，无解．
若a＝0，则l1：x＝1，l2：x＝，
显然l1∥l2，即由“l1∥l2”能推出“a＝0”．
综上所述a＝0⇔l1∥l2，所以p是q的充要条件．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
x)＝
＋
是R上的偶函数，求a的值．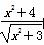
的最小值为2.
8，则△ABF2的周长为________．
顶点在坐标原点的抛物线的方程为__________．
，若函数g（x）=f（x）-k有两个不同的零点，则实数k的取值范围是______________________.