题目内容
已知椭圆: ,离心率为
,离心率为 ,焦点
,焦点 过
过 的直线交椭圆于
的直线交椭圆于 两点,且
两点,且 的周长为4.
的周长为4.
(Ⅰ)求椭圆方程;
(Ⅱ) 直线 与y轴交于点P(0,m)(m
与y轴交于点P(0,m)(m 0),与椭圆C交于相异两点A,B且
0),与椭圆C交于相异两点A,B且 .若
.若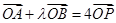 ,求m的取值范围。
,求m的取值范围。
 ,离心率为
,离心率为 ,焦点
,焦点 过
过 的直线交椭圆于
的直线交椭圆于 两点,且
两点,且 的周长为4.
的周长为4.(Ⅰ)求椭圆方程;
(Ⅱ) 直线
 与y轴交于点P(0,m)(m
与y轴交于点P(0,m)(m 0),与椭圆C交于相异两点A,B且
0),与椭圆C交于相异两点A,B且 .若
.若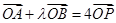 ,求m的取值范围。
,求m的取值范围。(Ⅰ)  ;(Ⅱ)
;(Ⅱ)
 ;(Ⅱ)
;(Ⅱ)
试题分析:(1)设C:
 (A>b>0),由条件知A-C=
(A>b>0),由条件知A-C= ,
, 由此能导出C的方程.(Ⅱ)由题意可知λ=3或O点与P点重合.当O点与P点重合时,m=0.当λ=3时,直线l与y轴相交,设l与椭圆C交点为A(x1,y1),B(x2,y2),
由此能导出C的方程.(Ⅱ)由题意可知λ=3或O点与P点重合.当O点与P点重合时,m=0.当λ=3时,直线l与y轴相交,设l与椭圆C交点为A(x1,y1),B(x2,y2), 得
得 再由根的判别式和韦达定理进行求解.
再由根的判别式和韦达定理进行求解.试题解析:(1)设C:
 (A>b>0),设C>0,
(A>b>0),设C>0, ,由条件知A-C=
,由条件知A-C= ,
, ,∴A=1,b=C=
,∴A=1,b=C= ,故C的方程为:
,故C的方程为: ;
;(Ⅱ)设
 与椭圆C的交点为A(
与椭圆C的交点为A( ,
, ),B(
),B( ,
, )。将y=kx+m代入
)。将y=kx+m代入
得
 ,所以
,所以 ①,
①, .因为
.因为 ,所以
,所以 ,
,消去
 得
得 ,所以
,所以 ,
,即
 ,当
,当 时,
时,
所以
 ,
, 由①得
由①得 ,解得
,解得

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
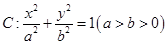 的左右焦点分别为
的左右焦点分别为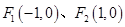 ,且经过点
,且经过点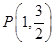 ,
,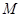 为椭圆上的动点,以
为椭圆上的动点,以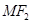 为半径作圆
为半径作圆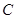 的方程;
的方程;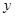 轴有两个交点,求点
轴有两个交点,求点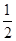 B.最小值
B.最小值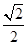 D.最小值
D.最小值 恒有公共点,则实数m的取值范围是( )
恒有公共点,则实数m的取值范围是( )



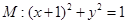 ,圆
,圆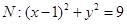 ,动圆
,动圆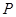 与圆
与圆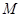 外切并且与圆
外切并且与圆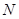 内切,圆心
内切,圆心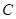 。
。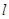 是与圆
是与圆 ,
,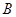 两点,当圆
两点,当圆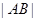 。
。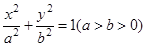 的离心率为
的离心率为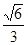 ,且过点
,且过点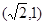 .
.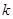 的直线
的直线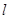 与椭圆相交于不同的两点
与椭圆相交于不同的两点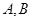 ,试问在
,试问在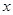 轴上是否存在点
轴上是否存在点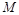 ,使
,使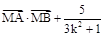 是与
是与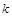 无关的常数?若存在,求出点
无关的常数?若存在,求出点 为椭圆
为椭圆 的两个焦点,P为椭圆上
的两个焦点,P为椭圆上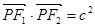 ,则此椭圆离心率的取值范围是 ( )
,则此椭圆离心率的取值范围是 ( )

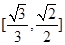
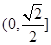
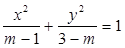 表示椭圆,则
表示椭圆,则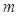 的取值范围是______________.
的取值范围是______________.