题目内容
已知椭圆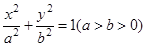 的离心率为
的离心率为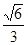 ,且过点
,且过点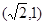 .
.
(1)求椭圆的方程;
(2)若过点C(-1,0)且斜率为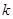 的直线
的直线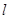 与椭圆相交于不同的两点
与椭圆相交于不同的两点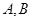 ,试问在
,试问在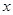 轴上是否存在点
轴上是否存在点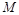 ,使
,使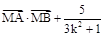 是与
是与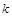 无关的常数?若存在,求出点
无关的常数?若存在,求出点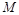 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
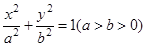 的离心率为
的离心率为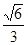 ,且过点
,且过点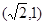 .
.(1)求椭圆的方程;
(2)若过点C(-1,0)且斜率为
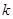 的直线
的直线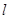 与椭圆相交于不同的两点
与椭圆相交于不同的两点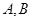 ,试问在
,试问在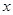 轴上是否存在点
轴上是否存在点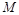 ,使
,使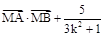 是与
是与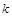 无关的常数?若存在,求出点
无关的常数?若存在,求出点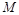 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(1)椭圆方程为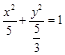 。
。
(2)在x轴上存在点M(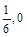 ), 使
), 使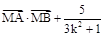 是与K无关的常数.
是与K无关的常数.
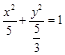 。
。(2)在x轴上存在点M(
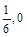 ), 使
), 使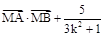 是与K无关的常数.
是与K无关的常数.试题分析:(1)∵椭圆离心率为
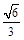 ,
,∴
 ,∴
,∴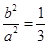 . 1分
. 1分又
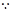 椭圆过点(
椭圆过点( ,1),代入椭圆方程,得
,1),代入椭圆方程,得 . 2分
. 2分所以
 . 4分
. 4分∴椭圆方程为
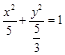 ,即
,即 . 5分
. 5分(2)在x轴上存在点M
 ,使
,使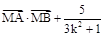 是与K无关的常数. 6分
是与K无关的常数. 6分证明:假设在x轴上存在点M(m,0),使
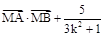 是与k无关的常数,
是与k无关的常数,∵直线L过点C(-1,0)且斜率为K,∴L方程为
 ,
,由
 得
得 . 7分
. 7分设
 ,则
,则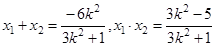 8分
8分∵
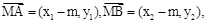
∴
 9分
9分=

=
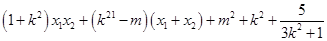
=
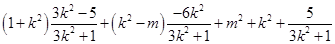
=
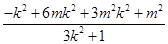 10分
10分设常数为t,则
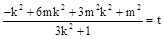 . 11分
. 11分整理得
 对任意的k恒成立,
对任意的k恒成立, 解得
解得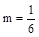 , 12分
, 12分即在x轴上存在点M(
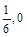 ), 使
), 使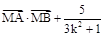 是与K无关的常数. 13分
是与K无关的常数. 13分点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。求椭圆标准方程时,主要运用了椭圆的几何性质,建立了a,bac的方程组。(2)作为研究
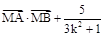 ,应用韦达定理,建立了m的函数式,利用函数观点,求得m的值,肯定存在性,使问题得解。
,应用韦达定理,建立了m的函数式,利用函数观点,求得m的值,肯定存在性,使问题得解。
练习册系列答案
相关题目
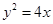 的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点
的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点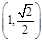 .
.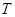
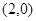 ,过点F2作直线
,过点F2作直线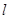 与椭圆C交于A,B两点,且
与椭圆C交于A,B两点,且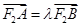 ,若
,若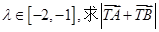 的取值范围.
的取值范围. ,离心率为
,离心率为 ,焦点
,焦点 过
过 的直线交椭圆于
的直线交椭圆于 两点,且
两点,且 的周长为4.
的周长为4. 与y轴交于点P(0,m)(m
与y轴交于点P(0,m)(m 0),与椭圆C交于相异两点A,B且
0),与椭圆C交于相异两点A,B且 .若
.若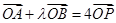 ,求m的取值范围。
,求m的取值范围。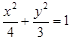 外的任意一点,过点P的直线PA、PB分别与椭圆相切于A、B两点。
外的任意一点,过点P的直线PA、PB分别与椭圆相切于A、B两点。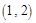 ,求直线
,求直线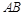 的方程。
的方程。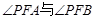 是否总是相等?若是,请给出证明。
是否总是相等?若是,请给出证明。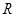 :
: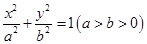 的长轴长为4,且过点
的长轴长为4,且过点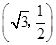 .
.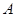 、
、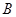 、
、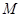 是椭圆上的三点,若
是椭圆上的三点,若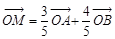 ,点
,点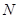 为线段
为线段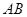 的中点,
的中点,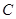 、
、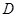 两点的坐标分别为
两点的坐标分别为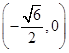 、
、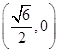 ,求证:
,求证: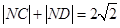 .
.
 的左顶点A且斜率为
的左顶点A且斜率为 的直线交椭圆
的直线交椭圆 于另一点
于另一点 ,且点
,且点 轴上的射影恰为右焦点
轴上的射影恰为右焦点 ,若
,若 ,则椭圆的离心率
,则椭圆的离心率 的值是 .
的值是 .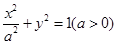 的左右焦点分别为F1,F2,P为椭圆上异于端点的任意的点,PF1,PF2的中点分别为M,N,O为坐标原点,四边形OMPN的周长为2
的左右焦点分别为F1,F2,P为椭圆上异于端点的任意的点,PF1,PF2的中点分别为M,N,O为坐标原点,四边形OMPN的周长为2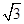 ,则△
,则△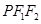 的周长是( )
的周长是( )



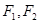 分别是椭圆
分别是椭圆 的左右焦点,过
的左右焦点,过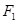 垂直与
垂直与 轴的直线交椭圆于
轴的直线交椭圆于 两点,若
两点,若 是锐角三角形,则椭圆离心率的范围是( )
是锐角三角形,则椭圆离心率的范围是( )



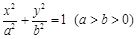 ,其离心率为
,其离心率为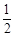 ,经过椭圆焦点且垂直于长轴的弦长为3.
,经过椭圆焦点且垂直于长轴的弦长为3.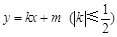 与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足
与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足 ,求
,求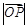 的取值范围.
的取值范围.